Structure optimization#
The optimization algorithms can be roughly divided into local optimization algorithms which find a nearby local minimum and global optimization algorithms that try to find the global minimum (a much harder task).
Most optimization algorithms available in ASE inherit the following
Optimizer base-class.
- class ase.optimize.optimize.Optimizer(atoms: Atoms, restart: str | None = None, logfile: IO | Path | str | None = None, trajectory: str | Path | None = None, append_trajectory: bool = False, **kwargs)[source]#
Base-class for all structure optimization classes.
- Parameters:
atoms (
Atoms) – The Atoms object to relax.restart (str) – Filename for restart file. Default value is None.
logfile (file object, Path, or str) – If logfile is a string, a file with that name will be opened. Use ‘-’ for stdout.
trajectory (Trajectory object, Path, or str) – Attach trajectory object. If trajectory is a string a Trajectory will be constructed. Use None for no trajectory.
append_trajectory (bool) – Appended to the trajectory file instead of overwriting it.
kwargs (dict, optional) – Extra arguments passed to
Dynamics.
Note
Optimizer classes themselves optimize only
internal atomic positions.
Cell volume and shape can also be optimized in combination with Filter
classes. (See Filters for details.)
Local optimization#
The local optimization algorithms available in ASE are: BFGS,
BFGSLineSearch, LBFGS, LBFGSLineSearch,
GPMin, MDMin and FIRE.
See also
Performance test for all ASE local optimizers.
MDMin and FIRE both use Newtonian dynamics with added
friction, to converge to an energy minimum, whereas the others are of
the quasi-Newton type, where the forces of consecutive steps are used
to dynamically update a Hessian describing the curvature of the
potential energy landscape. You can use the QuasiNewton synonym
for BFGSLineSearch because this algorithm is in many cases the optimal
of the quasi-Newton algorithms.
All of the local optimizer classes have the following structure:
class Optimizer:
def __init__(self, atoms, restart=None, logfile=None):
def run(self, fmax=0.05, steps=100000000):
def get_number_of_steps():
The convergence criterion is that the force on all individual atoms should be less than fmax:
BFGS#
The BFGS object is one of the minimizers in the ASE package. The below
script uses BFGS to optimize the structure of a water molecule, starting
with the experimental geometry:
from ase import Atoms
from ase.optimize import BFGS
from ase.calculators.emt import EMT
import numpy as np
d = 0.9575
t = np.pi / 180 * 104.51
water = Atoms('H2O',
positions=[(d, 0, 0),
(d * np.cos(t), d * np.sin(t), 0),
(0, 0, 0)],
calculator=EMT())
dyn = BFGS(water)
dyn.run(fmax=0.05)
which produces the following output. The columns are the solver name, step number, clock time, potential energy (eV), and maximum force.:
BFGS: 0 19:45:25 2.769633 8.6091
BFGS: 1 19:45:25 2.154560 4.4644
BFGS: 2 19:45:25 1.906812 1.3097
BFGS: 3 19:45:25 1.880255 0.2056
BFGS: 4 19:45:25 1.879488 0.0205
When doing structure optimization, it is useful to write the trajectory to a file, so that the progress of the optimization run can be followed during or after the run:
dyn = BFGS(water, trajectory='H2O.traj')
dyn.run(fmax=0.05)
Use the command ase gui H2O.traj to see what is going on (more here:
ase.gui). The trajectory file can also be accessed using the
module ase.io.trajectory.
The attach method takes an optional argument interval=n that can
be used to tell the structure optimizer object to write the
configuration to the trajectory file only every n steps.
During a structure optimization, the BFGS and LBFGS optimizers use two quantities to decide where to move the atoms on each step:
the forces on each atom, as returned by the associated
Calculatorobjectthe Hessian matrix, i.e. the matrix of second derivatives \(\frac{\partial^2 E}{\partial x_i \partial x_j}\) of the total energy with respect to nuclear coordinates.
If the atoms are close to the minimum, such that the potential energy surface is locally quadratic, the Hessian and forces accurately determine the required step to reach the optimal structure. The Hessian is very expensive to calculate a priori, so instead the algorithm estimates it by means of an initial guess which is adjusted along the way depending on the information obtained on each step of the structure optimization.
It is frequently practical to restart or continue a structure
optimization with a geometry obtained from a previous relaxation.
Aside from the geometry, the Hessian of the previous run can and
should be retained for the second run. Use the restart keyword to
specify a file in which to save the Hessian:
dyn = BFGS(atoms=system, trajectory='qn.traj', restart='qn.json')
This will create an optimizer which saves the Hessian to
qn.json (using the Python json module) on each
step. If the file already exists, the Hessian will also be
initialized from that file.
The trajectory file can also be used to restart a structure optimization, since it contains the history of all forces and positions, and thus whichever information about the Hessian was assembled so far:
dyn = BFGS(atoms=system, trajectory='qn.traj')
dyn.replay_trajectory('history.traj')
This will read through each iteration stored in history.traj,
performing adjustments to the Hessian as appropriate. Note that these
steps will not be written to qn.traj. If restarting with more than
one previous trajectory file, use ASE’s GUI to concatenate them
into a single trajectory file first:
$ ase gui part1.traj part2.traj -o history.traj
The file history.traj will then contain all necessary
information.
When switching between different types of optimizers, e.g. between
BFGS and LBFGS, the JSON-files specified by the
restart keyword are not compatible, but the Hessian can still be
retained by replaying the trajectory as above.
LBFGS#
LBFGS is the limited memory version of the BFGS algorithm, where
the inverse of Hessian matrix is updated instead of the Hessian
itself. Two ways exist for determining the atomic
step: Standard LBFGS and LBFGSLineSearch. For the
first one, both the directions and lengths of the atomic steps
are determined by the approximated Hessian matrix. While for the
latter one, the approximated Hessian matrix is only used to find
out the directions of the line searches and atomic steps, the
step lengths are determined by the forces.
To start a structure optimization with LBFGS algorithm is similar to BFGS. A typical optimization should look like:
dyn = LBFGS(atoms=system, trajectory='lbfgs.traj', restart='lbfgs.pckl')
where the trajectory and the restart save the trajectory of the optimization and the vectors needed to generate the Hessian Matrix.
GPMin#
The GPMin (Gaussian Process minimizer) produces a model for the Potential Energy Surface using the information about the potential energies and the forces of the configurations it has already visited and uses it to speed up BFGS local minimzations.
Read more about this algorithm here:
Estefanía Garijo del Río, Jens Jørgen Mortensen, Karsten W. JacobsenPhysical Review B, Vol. 100, 104103 (2019)
Warning
The memory of the optimizer scales as O(n²N²) where N is the number of atoms and n the number of steps. If the number of atoms is sufficiently high, this may cause a memory issue. This class prints a warning if the user tries to run GPMin with more than 100 atoms in the unit cell.
FIRE#
Read about this algorithm here:
Erik Bitzek, Pekka Koskinen, Franz Gähler, Michael Moseler, and Peter GumbschPhysical Review Letters, Vol. 97, 170201 (2006)
MDMin#
The MDmin algorithm is a modification of the usual velocity-Verlet molecular dynamics algorithm. Newtons second law is solved numerically, but after each time step the dot product between the forces and the momenta is checked. If it is zero, the system has just passed through a (local) minimum in the potential energy, the kinetic energy is large and about to decrease again. At this point, the momentum is set to zero. Unlike a “real” molecular dynamics, the masses of the atoms are not used, instead all masses are set to one.
The MDmin algorithm exists in two flavors, one where each atom is tested and stopped individually, and one where all coordinates are treated as one long vector, and all momenta are set to zero if the dot product between the momentum vector and force vector (both of length 3N) is zero. This module implements the latter version.
Although the algorithm is primitive, it performs very well because it takes advantage of the physics of the problem. Once the system is so near the minimum that the potential energy surface is approximately quadratic it becomes advantageous to switch to a minimization method with quadratic convergence, such as Conjugate Gradient or Quasi Newton.
SciPy optimizers#
SciPy provides a number of optimizers. An interface module for a couple of these have been written for ASE. Most notable are the optimizers SciPyFminBFGS and SciPyFminCG. These are called with the regular syntax and can be imported as:
from ase.optimize.sciopt import SciPyFminBFGS, SciPyFminCG
- class ase.optimize.sciopt.SciPyFminBFGS(atoms: Atoms, logfile: IO | str = '-', trajectory: str | None = None, callback_always: bool = False, alpha: float = 70.0, **kwargs)[source]#
Quasi-Newton method (Broydon-Fletcher-Goldfarb-Shanno)
Initialize object
- Parameters:
atoms (
Atoms) – The Atoms object to relax.trajectory (str) – Trajectory file used to store optimisation path.
logfile (file object or str) – If logfile is a string, a file with that name will be opened. Use ‘-’ for stdout.
callback_always (bool) – Should the callback be run after each force call (also in the linesearch)
alpha (float) – Initial guess for the Hessian (curvature of energy surface). A conservative value of 70.0 is the default, but number of needed steps to converge might be less if a lower value is used. However, a lower value also means risk of instability.
kwargs (dict, optional) – Extra arguments passed to
Optimizer.
- class ase.optimize.sciopt.SciPyFminCG(atoms: Atoms, logfile: IO | str = '-', trajectory: str | None = None, callback_always: bool = False, alpha: float = 70.0, **kwargs)[source]#
Non-linear (Polak-Ribiere) conjugate gradient algorithm
Initialize object
- Parameters:
atoms (
Atoms) – The Atoms object to relax.trajectory (str) – Trajectory file used to store optimisation path.
logfile (file object or str) – If logfile is a string, a file with that name will be opened. Use ‘-’ for stdout.
callback_always (bool) – Should the callback be run after each force call (also in the linesearch)
alpha (float) – Initial guess for the Hessian (curvature of energy surface). A conservative value of 70.0 is the default, but number of needed steps to converge might be less if a lower value is used. However, a lower value also means risk of instability.
kwargs (dict, optional) – Extra arguments passed to
Optimizer.
BFGSLineSearch#
- class ase.optimize.QuasiNewton#
BFGSLineSearch is the BFGS algorithm with a line search mechanism that enforces the step taken fulfills the Wolfe conditions, so that the energy and absolute value of the force decrease monotonically. Like the LBFGS algorithm the inverse of the Hessian Matrix is updated.
The usage of BFGSLineSearch algorithm is similar to other BFGS type algorithms. A typical optimization should look like:
from ase.optimize.bfgslinesearch import BFGSLineSearch
dyn = BFGSLineSearch(atoms=system, trajectory='bfgs_ls.traj', restart='bfgs_ls.pckl')
where the trajectory and the restart save the trajectory of the optimization and the information needed to generate the Hessian Matrix.
Note
In many of the examples, tests, exercises and tutorials,
QuasiNewton is used – it is a synonym for BFGSLineSearch.
The BFGSLineSearch algorithm is not compatible with nudged elastic band calculations.
Preconditioned optimizers#
Preconditioners can speed up optimization approaches by incorporating information about the local bonding topology into a redefined metric through a coordinate transformation. Preconditioners are problem dependent, but the general purpose-implementation in ASE provides a basis that can be adapted to achieve optimized performance for specific applications.
While the approach is general, the implementation is specific to a
given optimizer: currently LBFGS and FIRE can be preconditioned using
the ase.optimize.precon.lbfgs.PreconLBFGS and
ase.optimize.precon.fire.PreconFIRE classes, respectively.
You can read more about the theory and implementation here:
D. Packwood, J.R. Kermode; L. Mones, N. Bernstein, J. Woolley, N. Gould, C. Ortner and G. CsányiJ. Chem. Phys. 144, 164109 (2016).
Tests with a variety of solid-state systems using both DFT and classical
interatomic potentials driven though ASE calculators show speedup factors of up
to an order of magnitude for preconditioned L-BFGS over standard L-BFGS, and the
gain grows with system size. Precomputations are performed to automatically
estimate all parameters required. A linesearch based on enforcing only the first
Wolff condition (i.e. the Armijo sufficient descent condition) is also provided
in ase.utils.linesearcharmijo; this typically leads to a further speed up
when used in conjunction with the preconditioner.
For small systems, unless they are highly ill-conditioned due to large variations in bonding stiffness, it is unlikely that preconditioning provides a performance gain, and standard BFGS and LBFGS should be preferred. Therefore, for systems with fewer than 100 atoms, \(PreconLBFGS\) reverts to standard LBFGS. Preconditioning can be enforces with the keyword argument \(precon\).
The preconditioned L-BFGS method implemented in ASE does not require external
dependencies, but the scipy.sparse module can be used for efficient
sparse linear algebra, and the matscipy package is used for fast
computation of neighbour lists if available. The PyAMG package can be used to
efficiently invert the preconditioner using an adaptive multigrid method.
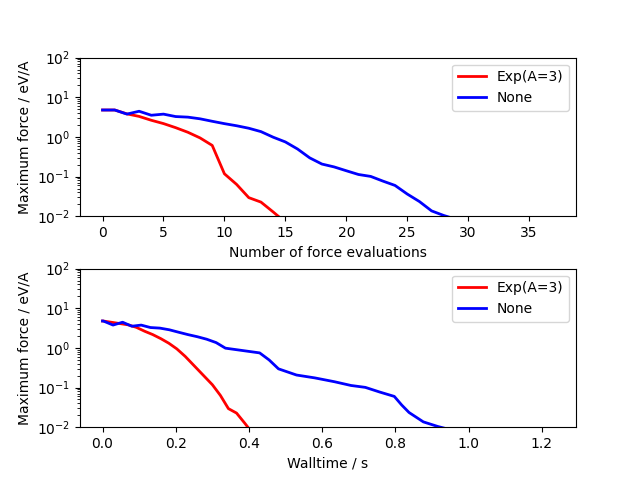
Usage is very similar to the standard optimizers. The example below compares unpreconditioned LBGFS with the default \(Exp\) preconditioner for a 3x3x3 bulk cube of copper containing a vacancy:
import numpy as np
from ase.build import bulk
from ase.calculators.emt import EMT
from ase.optimize.precon import Exp, PreconLBFGS
from ase.calculators.loggingcalc import LoggingCalculator
import matplotlib as mpl
mpl.use('Agg')
import matplotlib.pyplot as plt
a0 = bulk('Cu', cubic=True)
a0 *= [3, 3, 3]
del a0[0]
a0.rattle(0.1)
nsteps = []
energies = []
log_calc = LoggingCalculator(EMT())
for precon, label in zip([None, Exp(A=3)],
['None', 'Exp(A=3)']):
log_calc.label = label
atoms = a0.copy()
atoms.calc = log_calc
opt = PreconLBFGS(atoms, precon=precon, use_armijo=True)
opt.run(fmax=1e-3)
log_calc.plot(markers=['r-', 'b-'], energy=False, lw=2)
plt.savefig("precon_exp.png")
For molecular systems in gas phase the force field based \(FF\) preconditioner can be applied. An example below compares the effect of FF preconditioner to the unpreconditioned LBFGS for Buckminsterfullerene. Parameters are taken from Z. Berkai at al. Energy Procedia, 74, 2015, 59-64. and the underlying potential is computed using a standalone force field calculator:
import numpy as np
from ase.build import molecule
from ase.utils.ff import Morse, Angle, Dihedral, VdW
from ase.calculators.ff import ForceField
from ase.optimize.precon import get_neighbours, FF, PreconLBFGS
from ase.calculators.loggingcalc import LoggingCalculator
import matplotlib as mpl
mpl.use('Agg')
import matplotlib.pyplot as plt
a0 = molecule('C60')
a0.set_cell(50.0*np.identity(3))
neighbor_list = [[] for _ in range(len(a0))]
vdw_list = np.ones((len(a0), len(a0)), dtype=bool)
morses = []; angles = []; dihedrals = []; vdws = []
i_list, j_list, d_list, fixed_atoms = get_neighbours(atoms=a0, r_cut=1.5)
for i, j in zip(i_list, j_list):
neighbor_list[i].append(j)
for i in range(len(neighbor_list)):
neighbor_list[i].sort()
for i in range(len(a0)):
for jj in range(len(neighbor_list[i])):
j = neighbor_list[i][jj]
if j > i:
morses.append(Morse(atomi=i, atomj=j, D=6.1322, alpha=1.8502, r0=1.4322))
vdw_list[i, j] = vdw_list[j, i] = False
for kk in range(jj+1, len(neighbor_list[i])):
k = neighbor_list[i][kk]
angles.append(Angle(atomi=j, atomj=i, atomk=k, k=10.0, a0=np.deg2rad(120.0), cos=True))
vdw_list[j, k] = vdw_list[k, j] = False
for ll in range(kk+1, len(neighbor_list[i])):
l = neighbor_list[i][ll]
dihedrals.append(Dihedral(atomi=j, atomj=i, atomk=k, atoml=l, k=0.346))
for i in range(len(a0)):
for j in range(i+1, len(a0)):
if vdw_list[i, j]:
vdws.append(VdW(atomi=i, atomj=j, epsilonij=0.0115, rminij=3.4681))
log_calc = LoggingCalculator(ForceField(morses=morses, angles=angles, dihedrals=dihedrals, vdws=vdws))
for precon, label in zip([None, FF(morses=morses, angles=angles, dihedrals=dihedrals)],
['None', 'FF']):
log_calc.label = label
atoms = a0.copy()
atoms.calc = log_calc
opt = PreconLBFGS(atoms, precon=precon, use_armijo=True)
opt.run(fmax=1e-4)
log_calc.plot(markers=['r-', 'b-'], energy=False, lw=2)
plt.savefig("precon_ff.png")
For molecular crystals the \(Exp_FF\) preconditioner is recommended, which is a synthesis of \(Exp\) and \(FF\) preconditioners.
The ase.calculators.loggingcalc.LoggingCalculator provides
a convenient tool for plotting convergence and walltime.
Global optimization#
There are currently two global optimisation algorithms available.
Basin hopping#
The global optimization algorithm can be used quite similar as a local optimization algorithm:
from ase import *
from ase.optimize.basin import BasinHopping
bh = BasinHopping(atoms=system, # the system to optimize
temperature=100 * kB, # 'temperature' to overcome barriers
dr=0.5, # maximal stepwidth
optimizer=LBFGS, # optimizer to find local minima
fmax=0.1, # maximal force for the optimizer
)
Read more about this algorithm here:
David J. Wales and Jonathan P. K. DoyeJ. Phys. Chem. A, Vol. 101, 5111-5116 (1997)
and here:
David J. Wales and Harold A. ScheragaScience, Vol. 285, 1368 (1999)
Minima hopping#
The minima hopping algorithm was developed and described by Goedecker:
Stefan GoedeckerJ. Chem. Phys., Vol. 120, 9911 (2004)
This algorithm utilizes a series of alternating steps of NVE molecular dynamics and local optimizations, and has two parameters that the code dynamically adjusts in response to the progress of the search. The first parameter is the initial temperature of the NVE simulation. Whenever a step finds a new minimum this temperature is decreased; if the step finds a previously found minimum the temperature is increased. The second dynamically adjusted parameter is \(E_\mathrm{diff}\), which is an energy threshold for accepting a newly found minimum. If the new minimum is no more than \(E_\mathrm{diff}\) eV higher than the previous minimum, it is acccepted and \(E_\mathrm{diff}\) is decreased; if it is more than \(E_\mathrm{diff}\) eV higher it is rejected and \(E_\mathrm{diff}\) is increased. The method is used as:
from ase.optimize.minimahopping import MinimaHopping
opt = MinimaHopping(atoms=system)
opt(totalsteps=10)
This will run the algorithm until 10 steps are taken; alternatively, if totalsteps is not specified the algorithm will run indefinitely (or until stopped by a batch system). A number of optional arguments can be fed when initializing the algorithm as keyword pairs. The keywords and default values are:
T0: 1000., # K, initial MD ‘temperature’beta1: 1.1, # temperature adjustment parameterbeta2: 1.1, # temperature adjustment parameterbeta3: 1. / 1.1, # temperature adjustment parameterEdiff0: 0.5, # eV, initial energy acceptance thresholdalpha1: 0.98, # energy threshold adjustment parameteralpha2: 1. / 0.98, # energy threshold adjustment parametermdmin: 2, # criteria to stop MD simulation (no. of minima)logfile: ‘hop.log’, # text logminima_threshold: 0.5, # A, threshold for identical configstimestep: 1.0, # fs, timestep for MD simulationsoptimizer: QuasiNewton, # local optimizer to useminima_traj: ‘minima.traj’, # storage file for minima listfmax: 0.05, # eV/A, max force for optimizations
Specific definitions of the alpha, beta, and mdmin parameters can be found in the publication by Goedecker. minima_threshold is used to determine if two atomic configurations are identical; if any atom has moved by more than this amount it is considered a new configuration. Note that the code tries to do this in an intelligent manner: atoms are considered to be indistinguishable, and translations are allowed in the directions of the periodic boundary conditions. Therefore, if a CO is adsorbed in an ontop site on a (211) surface it will be considered identical no matter which ontop site it occupies.
The trajectory file minima_traj will be populated with the accepted minima as they are found. A log of the progress is kept in logfile.
The code is written such that a stopped simulation (e.g., killed by the batching system when the maximum wall time was exceeded) can usually be restarted without too much effort by the user. In most cases, the script can be resubmitted without any modification – if the logfile and minima_traj are found, the script will attempt to use these to resume. (Note that you may need to clean up files left in the directory by the calculator, however.)
Note that these searches can be quite slow, so it can pay to have multiple searches running at a time. Multiple searches can run in parallel and share one list of minima. (Run each script from a separate directory but specify the location to the same absolute location for minima_traj). Each search will use the global information of the list of minima, but will keep its own local information of the initial temperature and \(E_\mathrm{diff}\).
For an example of use, see the Constrained minima hopping (global optimization) tutorial.
Transition state search#
There are several strategies and tools for the search and optimization of
transition states available in ASE.
The transition state search and optimization algorithms are:
ClimbFixInternals, neb and dimer.
ClimbFixInternals#
The BFGSClimbFixInternals optimizer can be used to climb a reaction
coordinate defined using the FixInternals class.
- class ase.optimize.climbfixinternals.BFGSClimbFixInternals(atoms: ~ase.atoms.Atoms, restart: str | None = None, logfile: ~typing.IO | str = '-', trajectory: str | None = None, maxstep: float | None = None, alpha: float | None = None, climb_coordinate: ~typing.List[~ase.constraints.FixInternals] | None = None, optB: ~typing.Type[~ase.optimize.optimize.Optimizer] = <class 'ase.optimize.bfgs.BFGS'>, optB_kwargs: ~typing.Dict[str, ~typing.Any] | None = None, optB_fmax: float = 0.05, optB_fmax_scaling: float = 0.0, **kwargs)[source]#
Class for transition state search and optimization
Climbs the 1D reaction coordinate defined as constrained internal coordinate via the
FixInternalsclass while minimizing all remaining degrees of freedom.Details: Two optimizers, ‘A’ and ‘B’, are applied orthogonal to each other. Optimizer ‘A’ climbs the constrained coordinate while optimizer ‘B’ optimizes the remaining degrees of freedom after each climbing step. Optimizer ‘A’ uses the BFGS algorithm to climb along the projected force of the selected constraint. Optimizer ‘B’ can be any ASE optimizer (default: BFGS).
In combination with other constraints, the order of constraints matters. Generally, the FixInternals constraint should come first in the list of constraints. This has been tested with the
FixAtomsconstraint.Inspired by concepts described by P. N. Plessow. [1]
Note
Convergence is based on ‘fmax’ of the total forces which is the sum of the projected forces and the forces of the remaining degrees of freedom. This value is logged in the ‘logfile’. Optimizer ‘B’ logs ‘fmax’ of the remaining degrees of freedom without the projected forces. The projected forces can be inspected using the
get_projected_forces()method:>>> for _ in dyn.irun(): ... projected_forces = dyn.get_projected_forces()
Example
# fmt: off import numpy as np import pytest from ase.build import add_adsorbate, fcc100 from ase.calculators.emt import EMT from ase.constraints import FixAtoms, FixInternals from ase.optimize.climbfixinternals import BFGSClimbFixInternals from ase.vibrations import Vibrations def setup_atoms(): """Setup transition state search for the diffusion barrier for a Pt atom on a Pt surface.""" atoms = fcc100('Pt', size=(2, 2, 1), vacuum=10.0) add_adsorbate(atoms, 'Pt', 1.611, 'hollow') atoms.set_constraint(FixAtoms(list(range(4)))) # freeze the slab return atoms @pytest.mark.optimize() @pytest.mark.parametrize('scaling', [0.0, 0.01]) def test_climb_fix_internals(scaling, testdir): """Climb along the constrained bondcombo coordinate while optimizing the remaining degrees of freedom after each climbing step. For the definition of constrained internal coordinates see the documentation of the classes FixInternals and ClimbFixInternals.""" atoms = setup_atoms() atoms.calc = EMT() # Define reaction coordinate via linear combination of bond lengths reaction_coord = [[0, 4, 1.0], [1, 4, 1.0]] # 1 * bond_1 + 1 * bond_2 # Use current value `FixInternals.get_combo(atoms, reaction_coord)` # as initial value bondcombo = [None, reaction_coord] # 'None' will converts to current value atoms.set_constraint([FixInternals(bondcombos=[bondcombo])] + atoms.constraints) # Optimizer for transition state search along reaction coordinate opt = BFGSClimbFixInternals(atoms, climb_coordinate=reaction_coord, optB_fmax_scaling=scaling) opt.run(fmax=0.05) # Converge to a saddle point # Validate transition state by one imaginary vibrational mode vib = Vibrations(atoms, indices=[4]) vib.run() assert ((np.imag(vib.get_energies()) > 0) == [True, False, False]).all()
Allowed parameters are similar to the parent class
BFGSwith the following additions:- Parameters:
climb_coordinate (list) – Specifies which subconstraint of the
FixInternalsconstraint is to be climbed. Provide the corresponding nested list of indices (including coefficients in the case of Combo constraints). See the example above.optB (any ASE optimizer, optional) – Optimizer ‘B’ for optimization of the remaining degrees of freedom after each climbing step.
optB_kwargs (dict, optional) – Specifies keyword arguments to be passed to optimizer ‘B’ at its initialization. By default, optimizer ‘B’ writes a logfile and trajectory (optB_{…}.log, optB_{…}.traj) where {…} is the current value of the
climb_coordinate. Setlogfileto ‘-’ for console output. Settrajectoryto ‘None’ to suppress writing of the trajectory file.optB_fmax (float, optional) – Specifies the convergence criterion ‘fmax’ of optimizer ‘B’.
optB_fmax_scaling (float, optional) –
Scaling factor to dynamically tighten ‘fmax’ of optimizer ‘B’ to the value of
optB_fmaxwhen close to convergence. Can speed up the climbing process. The scaling formula is’fmax’ =
optB_fmax+optB_fmax_scaling\(\cdot\) norm_of_projected_forcesThe final optimization with optimizer ‘B’ is performed with
optB_fmaxindependent ofoptB_fmax_scaling.