Phonon calculations#
Module for calculating vibrational normal modes for periodic systems using the so-called small displacement method (see e.g. [Alfe]). So far, space-group symmetries are not exploited to reduce the number of atomic displacements that must be calculated and subsequent symmetrization of the force constants.
For polar materials the dynamical matrix at the zone center acquires a non-analytical contribution that accounts for the LO-TO splitting. This contribution requires additional functionality to evaluate and is not included in the present implementation. Its implementation in conjunction with the small displacement method is described in [Wang].
Example#
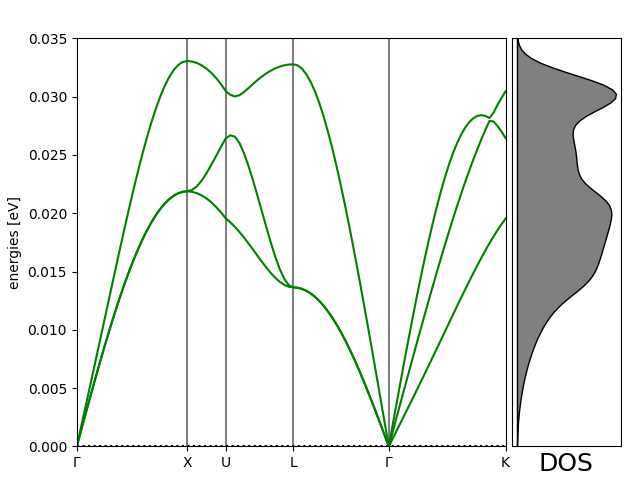
Simple example showing how to calculate the phonon dispersion for bulk aluminum using a 7x7x7 supercell within effective medium theory:
from ase.build import bulk
from ase.calculators.emt import EMT
from ase.phonons import Phonons
# Setup crystal and EMT calculator
atoms = bulk('Al', 'fcc', a=4.05)
# Phonon calculator
N = 7
ph = Phonons(atoms, EMT(), supercell=(N, N, N), delta=0.05)
ph.run()
# Read forces and assemble the dynamical matrix
ph.read(acoustic=True)
ph.clean()
path = atoms.cell.bandpath('GXULGK', npoints=100)
bs = ph.get_band_structure(path)
dos = ph.get_dos(kpts=(20, 20, 20)).sample_grid(npts=100, width=1e-3)
# Plot the band structure and DOS:
import matplotlib.pyplot as plt # noqa
fig = plt.figure(figsize=(7, 4))
ax = fig.add_axes([0.12, 0.07, 0.67, 0.85])
emax = 0.035
bs.plot(ax=ax, emin=0.0, emax=emax)
dosax = fig.add_axes([0.8, 0.07, 0.17, 0.85])
dosax.fill_between(
dos.get_weights(),
dos.get_energies(),
y2=0,
color='grey',
edgecolor='k',
lw=1,
)
dosax.set_ylim(0, emax)
dosax.set_yticks([])
dosax.set_xticks([])
dosax.set_xlabel('DOS', fontsize=18)
fig.savefig('Al_phonon.png')
Mode inspection:
# from ase.io.trajectory import Trajectory
# from ase.io import write
# Write modes for specific q-vector to trajectory files:
L = path.special_points['L']
ph.write_modes(
[l / 2 for l in L], branches=[2], repeat=(8, 8, 8), kT=3e-4, center=True
)
# Generate gif animation:
# XXX Temporarily disabled due to matplotlib writer compatibility issue.
# with Trajectory('phonon.mode.2.traj', 'r') as traj:
# write('Al_mode.gif', traj, interval=50,
# rotation='-36x,26.5y,-25z')
List of all Methods#
- class ase.phonons.Phonons(*args, **kwargs)[source]#
Class for calculating phonon modes using the finite displacement method.
The matrix of force constants is calculated from the finite difference approximation to the first-order derivative of the atomic forces as:
2 nbj nbj nbj d E F- - F+ C = ------------ ~ ------------- , mai dR dR 2 * delta mai nbj
where F+/F- denotes the force in direction j on atom nb when atom ma is displaced in direction +i/-i. The force constants are related by various symmetry relations. From the definition of the force constants it must be symmetric in the three indices mai:
nbj mai bj ai C = C -> C (R ) = C (-R ) . mai nbj ai n bj n
As the force constants can only depend on the difference between the m and n indices, this symmetry is more conveniently expressed as shown on the right hand-side.
The acoustic sum-rule:
_ _ aj \ bj C (R ) = - ) C (R ) ai 0 /__ ai m (m, b) != (0, a)
Ordering of the unit cells illustrated here for a 1-dimensional system (in case
refcell=Nonein constructor!):m = 0 m = 1 m = -2 m = -1 ----------------------------------------------------- | | | | | | * b | * | * | * | | | | | | | * a | * | * | * | | | | | | -----------------------------------------------------
Example:
>>> from ase.build import bulk >>> from ase.phonons import Phonons >>> from gpaw import GPAW, FermiDirac
>>> atoms = bulk('Si', 'diamond', a=5.4) >>> calc = GPAW(mode='fd', ... kpts=(5, 5, 5), ... h=0.2, ... occupations=FermiDirac(0.)) >>> ph = Phonons(atoms, calc, supercell=(5, 5, 5)) >>> ph.run() >>> ph.read(method='frederiksen', acoustic=True)
Initialize with base class args and kwargs.
- apply_cutoff(D_N, r_c)[source]#
Zero elements for interatomic distances larger than the cutoff.
Parameters:
- D_N: ndarray
Dynamical/force constant matrix.
- r_c: float
Cutoff in Angstrom.
- band_structure(path_kc, modes=False, born=False, verbose=True)[source]#
Calculate phonon dispersion along a path in the Brillouin zone.
The dynamical matrix at arbitrary q-vectors is obtained by Fourier transforming the real-space force constants. In case of negative eigenvalues (squared frequency), the corresponding negative frequency is returned.
Frequencies and modes are in units of eV and 1/sqrt(amu), respectively.
Parameters:
- path_kc: ndarray
List of k-point coordinates (in units of the reciprocal lattice vectors) specifying the path in the Brillouin zone for which the dynamical matrix will be calculated.
- modes: bool
Returns both frequencies and modes when True.
- born: bool
Include non-analytic part given by the Born effective charges and the static part of the high-frequency dielectric tensor. This contribution to the force constant accounts for the splitting between the LO and TO branches for q -> 0.
- verbose: bool
Print warnings when imaginary frequncies are detected.
Returns:
If modes=False: Array of energies
If modes=True: Tuple of two arrays with energies and modes.
- compute_dynamical_matrix(q_scaled: ndarray, D_N: ndarray)[source]#
- Computation of the dynamical matrix in momentum space D_ab(q).
This is a Fourier transform from real-space dynamical matrix D_N for a given momentum vector q.
q_scaled: q vector in scaled coordinates.
- D_N: the dynamical matrix in real-space. It is necessary, at least
currently, to provide this matrix explicitly (rather than use self.D_N) because this matrix is modified by the Born charges contributions and these modifications are momentum (q) dependent.
- Result:
- D(q): two-dimensional, complex-valued array of
shape=(3 * natoms, 3 * natoms).
- dos(kpts=(10, 10, 10), npts=1000, delta=0.001)[source]#
Calculate phonon dos as a function of energy.
Parameters:
- kpts: tuple
Shape of Monkhorst-Pack grid for sampling the Brillouin zone.
- npts: int
Number of energy points.
- delta: float
Broadening of Lorentzian line-shape in eV.
- Returns:
Tuple of (frequencies, dos). The frequencies are in units of eV.
Deprecated since version 3.23.1: Please use the
.get_dos()method instead, it returns a proper RawDOSData object.
- get_band_structure(path, modes=False, born=False, verbose=True)[source]#
Calculate and return the phonon band structure.
This method computes the phonon band structure for a given path in reciprocal space. It is a wrapper around the internal \(band_structure\) method of the \(Phonons\) class. The method can optionally calculate and return phonon modes.
Frequencies and modes are in units of eV and 1/sqrt(amu), respectively.
Parameters:
- pathBandPath object
The BandPath object defining the path in the reciprocal space over which the phonon band structure is calculated.
- modesbool, optional
If True, phonon modes will also be calculated and returned. Defaults to False.
- bornbool, optional
If True, includes the effect of Born effective charges in the phonon calculations. Defaults to False.
- verbosebool, optional
If True, enables verbose output during the calculation. Defaults to True.
Returns:
- BandStructure or tuple of (BandStructure, ndarray)
If
modesis False, returns aBandStructureobject containing the phonon band structure. Ifmodesis True, returns a tuple, where the first element is theBandStructureobject and the second element is an ndarray of phonon modes.If modes are returned, the array is of shape (k-point, bands, atoms, 3) and the norm-squared of the mode is \(1 / m_{eff}\), where \(m_{eff}\) is the effective mass of the mode.
Example:
>>> from ase.dft.kpoints import BandPath >>> path = BandPath(...) # Define the band path >>> phonons = Phonons(...) >>> bs, modes = phonons.get_band_structure(path, modes=True)
- get_dos(kpts=(10, 10, 10), indices=None, verbose=True)[source]#
Return a phonon density of states.
Parameters:
- kpts: tuple
Shape of Monkhorst-Pack grid for sampling the Brillouin zone.
- indices: list
If indices is not None, the amplitude-weighted atomic-partial DOS for the specified atoms will be calculated.
- verbose: bool
Print warnings when imaginary frequncies are detected.
- Returns:
A RawDOSData object containing the density of states.
- read(method='Frederiksen', symmetrize=3, acoustic=True, cutoff=None, born=False, **kwargs)[source]#
Read forces from json files and calculate force constants.
Extra keyword arguments will be passed to
read_born_charges.Parameters:
- method: str
Specify method for evaluating the atomic forces.
- symmetrize: int
Symmetrize force constants (see doc string at top) when
symmetrize != 0(default: 3). Since restoring the acoustic sum rule breaks the symmetry, the symmetrization must be repeated a few times until the changes a insignificant. The integer gives the number of iterations that will be carried out.- acoustic: bool
Restore the acoustic sum rule on the force constants.
- cutoff: None or float
Zero elements in the dynamical matrix between atoms with an interatomic distance larger than the cutoff.
- born: bool
Read in Born effective charge tensor and high-frequency static dielelctric tensor from file.
- read_born_charges(name='born', neutrality=True)[source]#
Read Born charges and dieletric tensor from JSON file.
The charge neutrality sum-rule:
_ _ \ a ) Z = 0 /__ ij a
Parameters:
- neutrality: bool
Restore charge neutrality condition on calculated Born effective charges.
- name: str
Key used to identify the file with Born charges for the unit cell in the JSON cache.
Deprecated since version 3.22.1: Current implementation of non-analytical correction is likely incorrect, see issue: #941
- write_modes(q_c, branches=0, kT=0.02585199101165164, born=False, repeat=(1, 1, 1), nimages=30, center=False)[source]#
Write modes to trajectory file.
Parameters:
- q_c: ndarray of shape (3,)
q-vector of the modes.
- branches: int or list
Branch index of modes.
- kT: float
Temperature in units of eV. Determines the amplitude of the atomic displacements in the modes.
- born: bool
Include non-analytic contribution to the force constants at q -> 0.
- repeat: tuple
Repeat atoms (l, m, n) times in the directions of the lattice vectors. Displacements of atoms in repeated cells carry a Bloch phase factor given by the q-vector and the cell lattice vector R_m.
- nimages: int
Number of images in an oscillation.
- center: bool
Center atoms in unit cell if True (default: False).
To exaggerate the amplitudes for better visualization, multiply kT by the square of the desired factor.
