X-ray scattering simulation

The module for simulation of X-ray scattering properties from the atomic level. The approach works only for finite systems, so that periodic boundary conditions and cell shape are ignored.

Theory

The scattering can be calculated using Debye formula [Debye1915] :

\[I(q) = \sum_{a, b} f_a(q) \cdot f_b(q) \cdot \frac{\sin(q \cdot r_{ab})}{q \cdot r_{ab}}\]

where:

• \(a\) and \(b\) – atom indexes;

• \(f_a(q)\) – \(a\)-th atomic scattering factor;

• \(r_{ab}\) – distance between atoms \(a\) and \(b\);

• \(q\) is a scattering vector length defined using scattering angle (\(\theta\)) and wavelength (\(\lambda\)) as \(q = 4\pi \cdot \sin(\theta)/\lambda\).

The thermal vibration of atoms can be accounted by introduction of damping exponent factor (Debye-Waller factor) written as \(\exp(-B \cdot q^2 / 2)\). The angular dependency of geometrical and polarization factors are expressed as [Iwasa2007] \(\cos(\theta)/(1 + \alpha \cos^2(2\theta))\), where \(\alpha \approx 1\) if incident beam is not polarized.

Units

The following measurement units are used:

• scattering vector \(q\) – inverse Angstrom (1/Å),

• thermal damping parameter \(B\) – squared Angstrom (Ų).

Example

The considered system is a nanoparticle of silver which is built using FaceCenteredCubic function (see ase.cluster) with parameters selected to produce approximately 2 nm sized particle:

from ase.cluster.cubic import FaceCenteredCubic
from ase.utils.xrdebye import XrDebye
import numpy as np

surfaces = [(1, 0, 0), (1, 1, 0), (1, 1, 1)]
atoms = FaceCenteredCubic('Ag', [(1, 0, 0), (1, 1, 0), (1, 1, 1)],
                          [6, 8, 8], 4.09)

Next, we need to specify the wavelength of the X-ray source:

xrd = XrDebye(atoms=atoms, wavelength=0.50523)

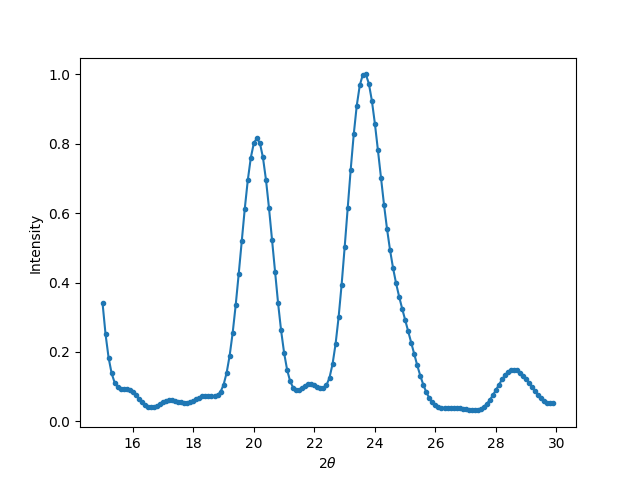
The X-ray diffraction pattern on the \(2\theta\) angles ranged from 15 to 30 degrees can be simulated as follows:

xrd.calc_pattern(x=np.arange(15, 30, 0.1), mode='XRD')
xrd.plot_pattern('xrd.png')

The resulted X-ray diffraction pattern shows (220) and (311) peaks at 20 and ~24 degrees respectively.

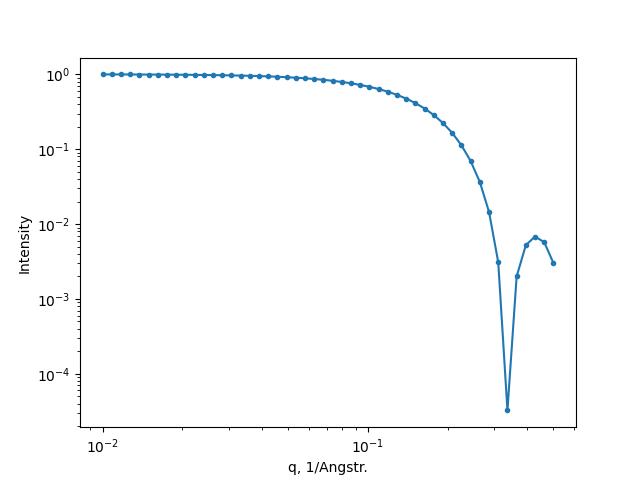
The small-angle scattering curve can be simulated too. Assuming that scattering vector is ranged from \(10^{-2}=0.01\) to \(10^{-0.3}\approx 0.5\) 1/Å the following code should be run:

xrd.calc_pattern(x=np.logspace(-2, -0.3, 50), mode='SAXS')
xrd.plot_pattern('saxs.png')

The resulted SAXS pattern:

Further details

The module contains wavelengths dictionary with X-ray wavelengths for copper and wolfram anodes:

from ase.utils.xrdebye import wavelengths
print('Cu Kalpha1 wavelength: %f Angstr.' % wavelengths['CuKa1'])

The dependence of atomic form-factors from scattering vector is calculated based on coefficients given in waasmaier dictionary according [Waasmaier1995] if method of calculations is set to ‘Iwasa’. In other case, the atomic factor is equal to atomic number and angular damping factor is omitted.

XrDebye class members

class ase.utils.xrdebye.XrDebye(atoms, wavelength, damping=0.04, method='Iwasa', alpha=1.01, warn=True)

Class for calculation of XRD or SAXS patterns.

Initilize the calculation of X-ray diffraction patterns

Parameters:

atoms: ase.Atoms

atoms object for which calculation will be performed.

wavelength: float, Angstrom

X-ray wavelength in Angstrom. Used for XRD and to setup dumpings.

dampingfloat, Angstrom**2

thermal damping factor parameter (B-factor).

method: {‘Iwasa’}

method of calculation (damping and atomic factors affected).

If set to ‘Iwasa’ than angular damping and q-dependence of atomic factors are used.

For any other string there will be only thermal damping and constant atomic factors (\(f_a(q) = Z_a\)).

alpha: float

parameter for angular damping of scattering intensity. Close to 1.0 for unplorized beam.

warn: boolean

flag to show warning if atomic factor can’t be calculated

calc_pattern(x=None, mode='XRD', verbose=False)

Calculate X-ray diffraction pattern or small angle X-ray scattering pattern.

Parameters:

x: float array

points where intensity will be calculated. XRD - 2theta values, in degrees; SAXS - q values in 1/A (\(q = 2 \pi \cdot s = 4 \pi \sin( \theta) / \lambda\)). If x is None then default values will be used.

mode: {‘XRD’, ‘SAXS’}

the mode of calculation: X-ray diffraction (XRD) or small-angle scattering (SAXS).

Returns:

list of intensities calculated for values given in x.

get(s)

Get the powder x-ray (XRD) scattering intensity using the Debye-Formula at single point.

Parameters:

s: float, in inverse Angstrom

scattering vector value (\(s = q / 2\pi\)).

Returns:

Intensity at given scattering vector \(s\).

get_waasmaier(symbol, s)

Scattering factor for free atoms.

Parameters:

symbol: string

atom element symbol.

s: float, in inverse Angstrom

scattering vector value (\(s = q / 2\pi\)).

Returns:

Intensity at given scattering vector \(s\).

Note

for hydrogen will be returned zero value.

plot_pattern(filename=None, show=False, ax=None)

Plot XRD or SAXS depending on filled data

Uses Matplotlib to plot pattern. Use show=True to show the figure and filename=’abc.png’ or filename=’abc.eps’ to save the figure to a file.

Returns:

matplotlib.axes.Axes object.

set_damping(damping)

set B-factor for thermal damping

write_pattern(filename)

Save calculated data to file specified by filename string.

References

[Debye1915]

16. Debye Ann. Phys. 351, 809–823 (1915)

[Iwasa2007]

20. Iwasa, K. Nobusada J. Phys. Chem. C, 111, 45-49 (2007) doi: 10.1021/jp063532w

[Waasmaier1995]

4. Waasmaier, A. Kirfel Acta Cryst. A51, 416-431 (1995)