Calculating Delta-values¶

In this tutorial we compare the equation-of-state (EOS) calculated for 7 FCC metals using values from EMT, WIEN2k and experiment. Each EOS is described by three parameters:

volume per atom
bulk-modulus
pressure derivative of bulk-modulus

Differences between two EOS’es can be measured by a single \(\Delta\) value defined as:

\[\sqrt{\frac{\int_{V_a}^{V_b} (E_1(V) - E_2(V))^2 dV} {V_b - V_a}},\]

where \(E_n(V)\) is the energy per atom as a function of volume. The \(\Delta\) value can be calculated using the ase.utils.deltacodesdft.delta() function:

ase.utils.deltacodesdft.delta(v1: float, B1: float, Bp1: float, v2: float, B2: float, Bp2: float, symmetric=True) → float[source]¶

Calculate Delta-value between two equation of states.

See also

Collection of ground-state elemental crystals: DeltaCodesDFT
Equation-of-state module: ase.eos

We get the WIEN2k and experimental numbers from the DeltaCodesDFT ASE-collection and we calculate the EMT EOS using this script:

from ase.calculators.emt import EMT
from ase.collections import dcdft
from ase.io import Trajectory

for symbol in ['Al', 'Ni', 'Cu', 'Pd', 'Ag', 'Pt', 'Au']:
    traj = Trajectory(f'{symbol}.traj', 'w')
    for s in range(94, 108, 2):
        atoms = dcdft[symbol]
        atoms.set_cell(atoms.cell * (s / 100)**(1 / 3), scale_atoms=True)
        atoms.calc = EMT()
        atoms.get_potential_energy()
        traj.write(atoms)

And fit to a Birch-Murnaghan EOS:

import json
from pathlib import Path
from typing import Tuple

from ase.eos import EquationOfState as EOS
from ase.io import read


def fit(symbol: str) -> Tuple[float, float, float, float]:
    V = []
    E = []
    for atoms in read(f'{symbol}.traj@:'):
        V.append(atoms.get_volume() / len(atoms))
        E.append(atoms.get_potential_energy() / len(atoms))
    eos = EOS(V, E, 'birchmurnaghan')
    eos.fit(warn=False)
    e0, B, Bp, v0 = eos.eos_parameters
    return e0, v0, B, Bp


data = {}  # Dict[str, Dict[str, float]]
for path in Path().glob('*.traj'):
    symbol = path.stem
    e0, v0, B, Bp = fit(symbol)
    data[symbol] = {'emt_energy': e0,
                    'emt_volume': v0,
                    'emt_B': B,
                    'emt_Bp': Bp}

Path('fit.json').write_text(json.dumps(data))

Result for Pt:

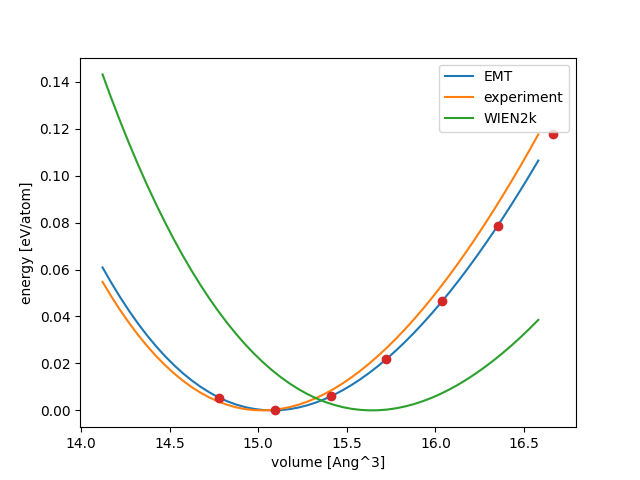
Volumes in Ang^3:

# symbol	emt	exp	wien2k
Al	15.93	16.27	16.48
Ni	10.60	10.81	10.89
Cu	11.57	11.65	11.95
Pd	14.59	14.56	15.31
Ag	16.77	16.85	17.85
Pt	15.08	15.02	15.64
Au	16.68	16.82	17.97

Bulk moduli in GPa:

# symbol	emt	exp	wien2k
Al	39.70	77.14	78.08
Ni	176.23	192.46	200.37
Cu	134.41	144.28	141.33
Pd	180.43	187.19	168.63
Ag	100.06	105.71	90.15
Pt	278.67	285.51	248.71
Au	174.12	182.01	139.11

Pressure derivative of bulk-moduli:

# symbol	emt	exp	wien2k
Al	2.72	4.45	4.57
Ni	3.76	4.00	5.00
Cu	4.21	4.88	4.86
Pd	5.17	5.00	5.56
Ag	4.75	4.72	5.42
Pt	5.31	5.18	5.46
Au	5.46	6.40	5.76

Now, we can calculate \(\Delta\) between EMT and WIEN2k for Pt:

>>> from ase.utils.deltacodesdft import delta
>>> from ase.units import kJ
>>> delta(15.08, 278.67 * 1e-24 * kJ, 5.31,
...       15.64, 248.71 * 1e-24 * kJ, 5.46)
0.03205389052984122

Here are all the values (in meV/atom) calculated with the script below:

# symbol	emt-exp	emt-wien2k	exp-wien2k
Al	5.9	8.6	3.6
Ni	8.6	12.5	3.7
Cu	2.7	11.9	9.5
Pd	1.0	27.6	29.0
Ag	1.9	22.4	21.3
Pt	3.5	32.2	35.9
Au	5.9	43.7	39.4

import json
from pathlib import Path

import matplotlib.pyplot as plt
import numpy as np

from ase.collections import dcdft
from ase.eos import birchmurnaghan
from ase.io import read
from ase.units import kJ
from ase.utils.deltacodesdft import delta

# Read EMT data:
data = json.loads(Path('fit.json').read_text())
# Insert values from experiment and WIEN2k:
for symbol in data:
    dcdft_dct = dcdft.data[symbol]
    dcdft_dct['exp_B'] *= 1e-24 * kJ
    dcdft_dct['wien2k_B'] *= 1e-24 * kJ
    data[symbol].update(dcdft_dct)

for name in ['volume', 'B', 'Bp']:
    with open(name + '.csv', 'w') as f:
        print('# symbol, emt, exp, wien2k', file=f)
        for symbol, dct in data.items():
            values = [dct[code + '_' + name]
                      for code in ['emt', 'exp', 'wien2k']]
            if name == 'B':
                values = [val * 1e24 / kJ for val in values]
            print(f'{symbol},',
                  ', '.join(f'{value:.2f}' for value in values),
                  file=f)

with open('delta.csv', 'w') as f:
    print('# symbol, emt-exp, emt-wien2k, exp-wien2k', file=f)
    for symbol, dct in data.items():
        # Get v0, B, Bp:
        emt, exp, wien2k = ((dct[code + '_volume'],
                             dct[code + '_B'],
                             dct[code + '_Bp'])
                            for code in ['emt', 'exp', 'wien2k'])
        print(f'{symbol},',
              '{:.1f}, {:.1f}, {:.1f}'.format(delta(*emt, *exp) * 1000,
                                              delta(*emt, *wien2k) * 1000,
                                              delta(*exp, *wien2k) * 1000),
              file=f)

        if symbol == 'Pt':
            va = min(emt[0], exp[0], wien2k[0])
            vb = max(emt[0], exp[0], wien2k[0])
            v = np.linspace(0.94 * va, 1.06 * vb)
            for (v0, B, Bp), code in [(emt, 'EMT'),
                                      (exp, 'experiment'),
                                      (wien2k, 'WIEN2k')]:
                plt.plot(v, birchmurnaghan(v, 0.0, B, Bp, v0), label=code)
            e0 = dct['emt_energy']
            V = []
            E = []
            for atoms in read('Pt.traj@:'):
                V.append(atoms.get_volume() / len(atoms))
                E.append(atoms.get_potential_energy() / len(atoms) - e0)
            plt.plot(V, E, 'o')
            plt.legend()
            plt.xlabel('volume [Ang^3]')
            plt.ylabel('energy [eV/atom]')
            plt.savefig('Pt.png')