The Atoms object#
The Atoms object is a collection of atoms. Here
is how to define a CO molecule:
from ase import Atoms
d = 1.1
co = Atoms('CO', positions=[(0, 0, 0), (0, 0, d)])
Here, the first argument specifies the type of the atoms and we used
the positions keywords to specify their positions. Other
possible keywords are: numbers, tags, momenta, masses,
magmoms and charges.
Here is how you could make an infinite gold wire with a bond length of 2.9 Å:
from ase import Atoms
d = 2.9
L = 10.0
wire = Atoms('Au',
positions=[[0, L / 2, L / 2]],
cell=[d, L, L],
pbc=[1, 0, 0])
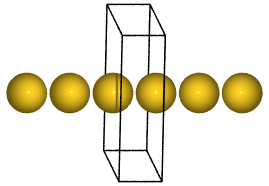
Here, two more optional keyword arguments were used:
cell: Unit cell sizeThis can be a sequence of three numbers for an orthorhombic unit cell or three by three numbers for a general unit cell (a sequence of three sequences of three numbers) or six numbers (three legths and three angles in degrees). The default value is [0,0,0] which is the same as [[0,0,0],[0,0,0],[0,0,0]] or [0,0,0,90,90,90] meaning that none of the three lattice vectors are defined.
pbc: Periodic boundary conditionsThe default value is False - a value of True would give periodic boundary conditions along all three axes. It is possible to give a sequence of three booleans to specify periodicity along specific axes.
You can also use the following methods to work with the unit cell and
the boundary conditions: set_pbc(),
set_cell(), get_cell(),
and get_pbc().
Working with the array methods of Atoms objects#
Like with a single Atom the properties of a collection of atoms
can be accessed and changed with get- and set-methods. For example
the positions of the atoms can be addressed as
>>> from ase import Atoms
>>> atoms = Atoms('N3', [(0, 0, 0), (1, 0, 0), (0, 0, 1)])
>>> atoms.get_positions()
array([[ 0., 0., 0.],
[ 1., 0., 0.],
[ 0., 0., 1.]])
>>> atoms.set_positions([(2, 0, 0), (0, 2, 2), (2, 2, 0)])
>>> atoms.get_positions()
array([[ 2., 0., 0.],
[ 0., 2., 2.],
[ 2., 2., 0.]])
Here is the full list of the get/set methods operating on all the
atoms at once. The get methods return an array of quantities, one for
each atom; the set methods take similar arrays.
E.g. get_positions() return N * 3 numbers,
get_atomic_numbers() return N integers.
These methods return copies of the internal arrays. It is thus safe to modify the returned arrays.
There are also a number of get/set methods that operate on quantities common to all the atoms or defined for the collection of atoms:
Unit cell and boundary conditions#
The Atoms object holds a unit cell. The unit cell
is a Cell object which resembles a 3x3 matrix
when used with numpy, arithmetic operations, or indexing:
>>> atoms.cell
Cell([0.0, 0.0, 0.0], pbc=False)
>>> atoms.cell[:]
array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
The cell can be defined or changed using the
set_cell() method. Changing the unit cell
does per default not move the atoms:
>>> import numpy as np
>>> atoms.set_cell(2 * np.identity(3))
>>> atoms.get_cell()
Cell([2.0, 2.0, 2.0], pbc=False)
>>> atoms.set_positions([(2, 0, 0), (1, 1, 0), (2, 2, 0)])
>>> atoms.get_positions()
array([[ 2., 0., 0.],
[ 1., 1., 0.],
[ 2., 2., 0.]])
However if we set scale_atoms=True the atomic positions are scaled with
the unit cell:
>>> atoms.set_cell(np.identity(3), scale_atoms=True)
>>> atoms.get_positions()
array([[ 1. , 0. , 0. ],
[ 0.5, 0.5, 0. ],
[ 1. , 1. , 0. ]])
The set_pbc() method specifies whether
periodic boundary conditions are to be used in the directions of the
three vectors of the unit cell. A slab calculation with periodic
boundary conditions in x and y directions and free boundary
conditions in the z direction is obtained through
>>> atoms.set_pbc((True, True, False))
or
>>> atoms.pbc = (True, True, False)
Special attributes#
It is also possible to work directly with the attributes
positions, numbers,
pbc and cell. Here
we change the position of the 2nd atom (which has count number 1
because Python starts counting at zero) and the type of the first
atom:
>>> atoms.positions *= 2
>>> atoms.positions[1] = (1, 1, 0)
>>> atoms.get_positions()
array([[ 2., 0., 0.],
[ 1., 1., 0.],
[ 2., 2., 0.]])
>>> atoms.positions
array([[ 2., 0., 0.],
[ 1., 1., 0.],
[ 2., 2., 0.]])
>>> atoms.numbers
array([7, 7, 7])
>>> atoms.numbers[0] = 13
>>> atoms.get_chemical_symbols()
['Al', 'N', 'N']
The atomic numbers can also be edited using the symbols
shortcut (see also ase.symbols.Symbols):
>>> atoms.symbols
Symbols('AlN2')
>>> atoms.symbols[2] = 'Cu'
>>> atoms.symbols
Symbols('AlNCu')
>>> atoms.numbers
array([13, 7, 29])
Check for periodic boundary conditions:
>>> atoms.pbc # equivalent to atoms.get_pbc()
array([ True, True, False], dtype=bool)
>>> atoms.pbc.any()
True
>>> atoms.pbc[2] = 1
>>> atoms.pbc
array([ True, True, True], dtype=bool)
Hexagonal unit cell:
>>> atoms.cell = [2.5, 2.5, 15, 90, 90, 120]
Attributes that can be edited directly are:
constraints()
Adding a calculator#
A calculator can be attached to the atoms with the purpose
of calculating energies and forces on the atoms. ASE works with many
different ase.calculators.
A calculator object calc is attached to the atoms like this:
>>> atoms.calc = calc
After the calculator has been appropriately setup the energy of the atoms can be obtained through
>>> atoms.get_potential_energy()
The term “potential energy” here means for example the total energy of a DFT calculation, which includes both kinetic, electrostatic, and exchange-correlation energy for the electrons. The reason it is called potential energy is that the atoms might also have a kinetic energy (from the moving nuclei) and that is obtained with
>>> atoms.get_kinetic_energy()
In case of a DFT calculator, it is up to the user to check exactly what
the get_potential_energy() method returns. For
example it may be the result of a calculation with a finite
temperature smearing of the occupation numbers extrapolated to zero
temperature. More about this can be found for the different
ase.calculators.
The following methods can only be called if a calculator is present:
Not all of these methods are supported by all calculators.
List-methods#
method |
example |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Note that the del method can be used with the more powerful numpy-style indexing, as in the second example above. This can be combined with python list comprehension in order to selectively delete atoms within an ASE Atoms object. For example, the below code creates an ethanol molecule and subsequently strips all the hydrogen atoms from it:
from ase.build import molecule
atoms = molecule('CH3CH2OH')
del atoms[[atom.index for atom in atoms if atom.symbol=='H']]
Other methods#
List of all Methods#
- class ase.Atoms(symbols=None, positions=None, numbers=None, tags=None, momenta=None, masses=None, magmoms=None, charges=None, scaled_positions=None, cell=None, pbc=None, celldisp=None, constraint=None, calculator=None, info=None, velocities=None)[source]#
Atoms object.
The Atoms object can represent an isolated molecule, or a periodically repeated structure. It has a unit cell and there may be periodic boundary conditions along any of the three unit cell axes. Information about the atoms (atomic numbers and position) is stored in ndarrays. Optionally, there can be information about tags, momenta, masses, magnetic moments and charges.
In order to calculate energies, forces and stresses, a calculator object has to attached to the atoms object.
- Parameters:
symbols (str | list[str] | list[Atom]) –
Chemical formula, a list of chemical symbols, or list of
Atomobjects (mutually exclusive withnumbers).'H2O''COPt12'['H', 'H', 'O'][Atom('Ne', (x, y, z)), ...]
positions (list[tuple[float, float, float]]) – Atomic positions in Cartesian coordinates (mutually exclusive with
scaled_positions). Anything that can be converted to an ndarray of shape (n, 3) works: [(x0, y0, z0), (x1, y1, z1), …].scaled_positions (list[tuple[float, float, float]]) – Atomic positions in units of the unit cell (mutually exclusive with
positions).numbers (list[int]) – Atomic numbers (mutually exclusive with
symbols).momenta (list[tuple[float, float, float]]) – Momenta for all atoms in Cartesian coordinates (mutually exclusive with
velocities).velocities (list[tuple[float, float, float]]) – Velocities for all atoms in Cartesian coordinates (mutually exclusive with
momenta).magmoms (list[float] | list[tuple[float, float, float]]) – Magnetic moments. Can be either a single value for each atom for collinear calculations or three numbers for each atom for non-collinear calculations.
cell (3x3 matrix or length 3 or 6 vector, default: (0, 0, 0)) – Unit cell vectors. Can also be given as just three numbers for orthorhombic cells, or 6 numbers, where first three are lengths of unit cell vectors, and the other three are angles between them (in degrees), in following order: [len(a), len(b), len(c), angle(b,c), angle(a,c), angle(a,b)]. First vector will lie in x-direction, second in xy-plane, and the third one in z-positive subspace.
celldisp (tuple[float, float, float], default: (0, 0, 0)) – Unit cell displacement vector. To visualize a displaced cell around the center of mass of a Systems of atoms.
pbc (bool | tuple[bool, bool, bool], default: False) –
Periodic boundary conditions flags.
TrueFalse01(1, 1, 0)(True, False, False)
constraint (constraint object(s)) – One or more ASE constraints applied during structure optimization.
calculator (calculator object) – ASE calculator to obtain energies and atomic forces.
info (dict | None, default: None) –
Dictionary with additional information about the system. The following keys may be used by ASE:
spacegroup:
Spacegroupinstanceunit_cell: ‘conventional’ | ‘primitive’ | int | 3 ints
adsorbate_info: Information about special adsorption sites
Items in the info attribute survives copy and slicing and can be stored in and retrieved from trajectory files given that the key is a string, the value is JSON-compatible and, if the value is a user-defined object, its base class is importable. One should not make any assumptions about the existence of keys.
Examples
>>> from ase import Atom
N2 molecule (These three are equivalent):
>>> d = 1.104 # N2 bondlength >>> a = Atoms('N2', [(0, 0, 0), (0, 0, d)]) >>> a = Atoms(numbers=[7, 7], positions=[(0, 0, 0), (0, 0, d)]) >>> a = Atoms([Atom('N', (0, 0, 0)), Atom('N', (0, 0, d))])
FCC gold:
>>> a = 4.05 # Gold lattice constant >>> b = a / 2 >>> fcc = Atoms('Au', ... cell=[(0, b, b), (b, 0, b), (b, b, 0)], ... pbc=True)
Hydrogen wire:
>>> d = 0.9 # H-H distance >>> h = Atoms('H', positions=[(0, 0, 0)], ... cell=(d, 0, 0), ... pbc=(1, 0, 0))
- property calc#
Calculator object.
- property cell#
The
ase.cell.Cellfor direct manipulation.
- center(vacuum=None, axis=(0, 1, 2), about=None)[source]#
Center atoms in unit cell.
Centers the atoms in the unit cell, so there is the same amount of vacuum on all sides.
- vacuum: float (default: None)
If specified adjust the amount of vacuum when centering. If vacuum=10.0 there will thus be 10 Angstrom of vacuum on each side.
- axis: int or sequence of ints
Axis or axes to act on. Default: Act on all axes.
- about: float or array (default: None)
If specified, center the atoms about <about>. I.e., about=(0., 0., 0.) (or just “about=0.”, interpreted identically), to center about the origin.
- edit()[source]#
Modify atoms interactively through ASE’s GUI viewer.
Conflicts leading to undesirable behaviour might arise when matplotlib has been pre-imported with certain incompatible backends and while trying to use the plot feature inside the interactive GUI. To circumvent, please set matplotlib.use(‘gtk’) before calling this method.
- euler_rotate(phi: float = 0.0, theta: float = 0.0, psi: float = 0.0, center: Sequence[float] = (0.0, 0.0, 0.0)) None[source]#
Rotate atoms via Euler angles (in degrees).
See e.g http://mathworld.wolfram.com/EulerAngles.html for explanation.
Note that the rotations in this method are passive and applied not to the atomic coordinates in the present frame but the frame itself.
- Parameters:
phi (float) – The 1st rotation angle around the z axis.
theta (float) – Rotation around the x axis.
psi (float) – 2nd rotation around the z axis.
center (Sequence[float], default = (0.0, 0.0, 0.0)) – The point to rotate about. A sequence of length 3 with the coordinates, or ‘COM’ to select the center of mass, ‘COP’ to select center of positions or ‘COU’ to select center of cell.
- get_all_distances(mic=False, vector=False)[source]#
Return distances of all of the atoms with all of the atoms.
Use mic=True to use the Minimum Image Convention.
- get_angle(a1, a2, a3, mic=False)[source]#
Get angle formed by three atoms.
Calculate angle in degrees between the vectors a2->a1 and a2->a3.
Use mic=True to use the Minimum Image Convention and calculate the angle across periodic boundaries.
- get_angles(indices, mic=False)[source]#
Get angle formed by three atoms for multiple groupings.
Calculate angle in degrees between vectors between atoms a2->a1 and a2->a3, where a1, a2, and a3 are in each row of indices.
Use mic=True to use the Minimum Image Convention and calculate the angle across periodic boundaries.
- get_array(name, copy=True)[source]#
Get an array.
Returns a copy unless the optional argument copy is false.
- get_calculator()[source]#
Get currently attached calculator object.
Deprecated since version 3.20.0: Please use the equivalent
atoms.calcinstead ofatoms.get_calculator().
- get_cell(complete=False)[source]#
Get the three unit cell vectors as a \(class\):ase.cell.Cell` object.
The Cell object resembles a 3x3 ndarray, and cell[i, j] is the jth Cartesian coordinate of the ith cell vector.
- get_cell_lengths_and_angles()[source]#
Get unit cell parameters. Sequence of 6 numbers.
First three are unit cell vector lengths and second three are angles between them:
[len(a), len(b), len(c), angle(b,c), angle(a,c), angle(a,b)]
in degrees.
Deprecated since version 3.21.0: Please use
atoms.cell.cellpar()instead
- get_chemical_formula(mode='hill', empirical=False)[source]#
Get the chemical formula as a string based on the chemical symbols.
Parameters:
- mode: str
There are four different modes available:
‘all’: The list of chemical symbols are contracted to a string, e.g. [‘C’, ‘H’, ‘H’, ‘H’, ‘O’, ‘H’] becomes ‘CHHHOH’.
‘reduce’: The same as ‘all’ where repeated elements are contracted to a single symbol and a number, e.g. ‘CHHHOCHHH’ is reduced to ‘CH3OCH3’.
‘hill’: The list of chemical symbols are contracted to a string following the Hill notation (alphabetical order with C and H first), e.g. ‘CHHHOCHHH’ is reduced to ‘C2H6O’ and ‘SOOHOHO’ to ‘H2O4S’. This is default.
‘metal’: The list of chemical symbols (alphabetical metals, and alphabetical non-metals)
- empirical, bool (optional, default=False)
Divide the symbol counts by their greatest common divisor to yield an empirical formula. Only for mode \(metal\) and \(hill\).
- get_chemical_symbols()[source]#
Get list of chemical symbol strings.
Equivalent to
list(atoms.symbols).
- get_dihedral(a0, a1, a2, a3, mic=False)[source]#
Calculate dihedral angle.
Calculate dihedral angle (in degrees) between the vectors a0->a1 and a2->a3.
Use mic=True to use the Minimum Image Convention and calculate the angle across periodic boundaries.
- get_dihedrals(indices, mic=False)[source]#
Calculate dihedral angles.
Calculate dihedral angles (in degrees) between the list of vectors a0->a1 and a2->a3, where a0, a1, a2 and a3 are in each row of indices.
Use mic=True to use the Minimum Image Convention and calculate the angles across periodic boundaries.
- get_dipole_moment()[source]#
Calculate the electric dipole moment for the atoms object.
Only available for calculators which has a get_dipole_moment() method.
- get_distance(a0, a1, mic=False, vector=False)[source]#
Return distance between two atoms.
Use mic=True to use the Minimum Image Convention. vector=True gives the distance vector (from a0 to a1).
- get_distances(a, indices, mic=False, vector=False)[source]#
Return distances of atom No.i with a list of atoms.
Use mic=True to use the Minimum Image Convention. vector=True gives the distance vector (from a to self[indices]).
- get_forces(apply_constraint=True, md=False)[source]#
Calculate atomic forces.
Ask the attached calculator to calculate the forces and apply constraints. Use apply_constraint=False to get the raw forces.
For molecular dynamics (md=True) we don’t apply the constraint to the forces but to the momenta. When holonomic constraints for rigid linear triatomic molecules are present, ask the constraints to redistribute the forces within each triple defined in the constraints (required for molecular dynamics with this type of constraints).
- get_global_number_of_atoms()[source]#
Returns the global number of atoms in a distributed-atoms parallel simulation.
DO NOT USE UNLESS YOU KNOW WHAT YOU ARE DOING!
Equivalent to len(atoms) in the standard ASE Atoms class. You should normally use len(atoms) instead. This function’s only purpose is to make compatibility between ASE and Asap easier to maintain by having a few places in ASE use this function instead. It is typically only when counting the global number of degrees of freedom or in similar situations.
- get_kinetic_stresses(voigt=True)[source]#
Calculate the kinetic part of the Virial stress of all the atoms.
- get_moments_of_inertia(vectors=False)[source]#
Get the moments of inertia along the principal axes.
The three principal moments of inertia are computed from the eigenvalues of the symmetric inertial tensor. Periodic boundary conditions are ignored. Units of the moments of inertia are amu*angstrom**2.
- get_number_of_atoms()[source]#
Deprecated since version 3.18.1: You probably want
len(atoms). Or if your atoms are distributed, use (and see)get_global_number_of_atoms().
- get_number_of_degrees_of_freedom()[source]#
Calculate the number of degrees of freedom in the system.
- get_positions(wrap=False, **wrap_kw)[source]#
Get array of positions.
Parameters:
- wrap: bool
wrap atoms back to the cell before returning positions
- wrap_kw: (keyword=value) pairs
optional keywords \(pbc\), \(center\), \(pretty_translation\), \(eps\), see
ase.geometry.wrap_positions()
- get_potential_energies()[source]#
Calculate the potential energies of all the atoms.
Only available with calculators supporting per-atom energies (e.g. classical potentials).
- get_potential_energy(force_consistent=False, apply_constraint=True)[source]#
Calculate potential energy.
Ask the attached calculator to calculate the potential energy and apply constraints. Use apply_constraint=False to get the raw forces.
When supported by the calculator, either the energy extrapolated to zero Kelvin or the energy consistent with the forces (the free energy) can be returned.
- get_reciprocal_cell()[source]#
Get the three reciprocal lattice vectors as a 3x3 ndarray.
Note that the commonly used factor of 2 pi for Fourier transforms is not included here.
Deprecated since version 3.21.0: Please use
atoms.cell.reciprocal()
- get_scaled_positions(wrap=True)[source]#
Get positions relative to unit cell.
If wrap is True, atoms outside the unit cell will be wrapped into the cell in those directions with periodic boundary conditions so that the scaled coordinates are between zero and one.
If any cell vectors are zero, the corresponding coordinates are evaluated as if the cell were completed using
cell.complete(). This means coordinates will be Cartesian as long as the non-zero cell vectors span a Cartesian axis or plane.
- get_stress(voigt=True, apply_constraint=True, include_ideal_gas=False)[source]#
Calculate stress tensor.
Returns an array of the six independent components of the symmetric stress tensor, in the traditional Voigt order (xx, yy, zz, yz, xz, xy) or as a 3x3 matrix. Default is Voigt order.
The ideal gas contribution to the stresses is added if the atoms have momenta and
include_ideal_gasis set to True.
- get_stresses(include_ideal_gas=False, voigt=True)[source]#
Calculate the stress-tensor of all the atoms.
Only available with calculators supporting per-atom energies and stresses (e.g. classical potentials). Even for such calculators there is a certain arbitrariness in defining per-atom stresses.
The ideal gas contribution to the stresses is added if the atoms have momenta and
include_ideal_gasis set to True.
- has(name)[source]#
Check for existence of array.
name must be one of: ‘tags’, ‘momenta’, ‘masses’, ‘initial_magmoms’, ‘initial_charges’.
- new_array(name, a, dtype=None, shape=None)[source]#
Add new array.
If shape is not None, the shape of a will be checked.
- property number_of_lattice_vectors#
Number of (non-zero) lattice vectors.
Deprecated since version 3.21.0: Please use
atoms.cell.rankinstead
- property numbers#
Attribute for direct manipulation of the atomic numbers.
- property pbc#
Reference to pbc-flags for in-place manipulations.
- property positions#
Attribute for direct manipulation of the positions.
- rattle(stdev=0.001, seed=None, rng=None)[source]#
Randomly displace atoms.
This method adds random displacements to the atomic positions, taking a possible constraint into account. The random numbers are drawn from a normal distribution of standard deviation stdev.
By default, the random number generator always uses the same seed (42) for repeatability. You can provide your own seed (an integer), or if you want the randomness to be different each time you run a script, then provide \(rng=numpy.random\). For a parallel calculation, it is important to use the same seed on all processors!
- repeat(rep)[source]#
Create new repeated atoms object.
The rep argument should be a sequence of three positive integers like (2,3,1) or a single integer (r) equivalent to (r,r,r).
- rotate(a, v, center=(0, 0, 0), rotate_cell=False)[source]#
Rotate atoms based on a vector and an angle, or two vectors.
Parameters:
- a = None:
Angle that the atoms is rotated around the vector ‘v’. ‘a’ can also be a vector and then ‘a’ is rotated into ‘v’.
- v:
Vector to rotate the atoms around. Vectors can be given as strings: ‘x’, ‘-x’, ‘y’, … .
- center = (0, 0, 0):
The center is kept fixed under the rotation. Use ‘COM’ to fix the center of mass, ‘COP’ to fix the center of positions or ‘COU’ to fix the center of cell.
- rotate_cell = False:
If true the cell is also rotated.
Examples:
Rotate 90 degrees around the z-axis, so that the x-axis is rotated into the y-axis:
>>> atoms = Atoms() >>> atoms.rotate(90, 'z') >>> atoms.rotate(90, (0, 0, 1)) >>> atoms.rotate(-90, '-z') >>> atoms.rotate('x', 'y') >>> atoms.rotate((1, 0, 0), (0, 1, 0))
- rotate_dihedral(a1, a2, a3, a4, angle, mask=None, indices=None)[source]#
Rotate dihedral angle.
Same usage as in
ase.Atoms.set_dihedral(): Rotate a group by a predefined dihedral angle, starting from its current configuration.
- set_angle(a1, a2=None, a3=None, angle=None, mask=None, indices=None, add=False)[source]#
Set angle (in degrees) formed by three atoms.
Sets the angle between vectors a2->*a1* and a2->*a3*.
If add is \(True\), the angle will be changed by the value given.
Same usage as in
ase.Atoms.set_dihedral(). If mask and indices are given, indices overwrites mask. If mask and indices are not set, only a3 is moved.
- set_array(name, a, dtype=None, shape=None)[source]#
Update array.
If shape is not None, the shape of a will be checked. If a is None, then the array is deleted.
- set_calculator(calc=None)[source]#
Attach calculator object.
Deprecated since version 3.20.0: Please use the equivalent
atoms.calc = calcinstead of this method.
- set_cell(cell, scale_atoms=False, apply_constraint=True)[source]#
Set unit cell vectors.
Parameters:
- cell: 3x3 matrix or length 3 or 6 vector
Unit cell. A 3x3 matrix (the three unit cell vectors) or just three numbers for an orthorhombic cell. Another option is 6 numbers, which describes unit cell with lengths of unit cell vectors and with angles between them (in degrees), in following order: [len(a), len(b), len(c), angle(b,c), angle(a,c), angle(a,b)]. First vector will lie in x-direction, second in xy-plane, and the third one in z-positive subspace.
- scale_atoms: bool
Fix atomic positions or move atoms with the unit cell? Default behavior is to not move the atoms (scale_atoms=False).
- apply_constraint: bool
Whether to apply constraints to the given cell.
Examples:
Two equivalent ways to define an orthorhombic cell:
>>> atoms = Atoms('He') >>> a, b, c = 7, 7.5, 8 >>> atoms.set_cell([a, b, c]) >>> atoms.set_cell([(a, 0, 0), (0, b, 0), (0, 0, c)])
FCC unit cell:
>>> atoms.set_cell([(0, b, b), (b, 0, b), (b, b, 0)])
Hexagonal unit cell:
>>> atoms.set_cell([a, a, c, 90, 90, 120])
Rhombohedral unit cell:
>>> alpha = 77 >>> atoms.set_cell([a, a, a, alpha, alpha, alpha])
- set_center_of_mass(com, scaled=False)[source]#
Set the center of mass.
If scaled=True the center of mass is expected in scaled coordinates. Constraints are considered for scaled=False.
- set_constraint(constraint=None)[source]#
Apply one or more constrains.
The constraint argument must be one constraint object or a list of constraint objects.
- set_dihedral(a1, a2, a3, a4, angle, mask=None, indices=None)[source]#
Set the dihedral angle (degrees) between vectors a1->a2 and a3->a4 by changing the atom indexed by a4.
If mask is not None, all the atoms described in mask (read: the entire subgroup) are moved. Alternatively to the mask, the indices of the atoms to be rotated can be supplied. If both mask and indices are given, indices overwrites mask.
Important: If mask or indices is given and does not contain a4, a4 will NOT be moved. In most cases you therefore want to include a4 in mask/indices.
Example: the following defines a very crude ethane-like molecule and twists one half of it by 30 degrees.
>>> atoms = Atoms('HHCCHH', [[-1, 1, 0], [-1, -1, 0], [0, 0, 0], ... [1, 0, 0], [2, 1, 0], [2, -1, 0]]) >>> atoms.set_dihedral(1, 2, 3, 4, 210, mask=[0, 0, 0, 1, 1, 1])
- set_distance(a0, a1, distance, fix=0.5, mic=False, mask=None, indices=None, add=False, factor=False)[source]#
Set the distance between two atoms.
Set the distance between atoms a0 and a1 to distance. By default, the center of the two atoms will be fixed. Use fix=0 to fix the first atom, fix=1 to fix the second atom and fix=0.5 (default) to fix the center of the bond.
If mask or indices are set (mask overwrites indices), only the atoms defined there are moved (see
ase.Atoms.set_dihedral()).When add is true, the distance is changed by the value given. In combination with factor True, the value given is a factor scaling the distance.
It is assumed that the atoms in mask/indices move together with a1. If fix=1, only a0 will therefore be moved.
- set_initial_magnetic_moments(magmoms=None)[source]#
Set the initial magnetic moments.
Use either one or three numbers for every atom (collinear or non-collinear spins).
- set_masses(masses='defaults')[source]#
Set atomic masses in atomic mass units.
The array masses should contain a list of masses. In case the masses argument is not given or for those elements of the masses list that are None, standard values are set.
- set_positions(newpositions, apply_constraint=True)[source]#
Set positions, honoring any constraints. To ignore constraints, use apply_constraint=False.
- set_tags(tags)[source]#
Set tags for all atoms. If only one tag is supplied, it is applied to all atoms.
- property symbols#
Get chemical symbols as a
ase.symbols.Symbolsobject.The object works like
atoms.numbersexcept its values are strings. It supports in-place editing.
- translate(displacement)[source]#
Translate atomic positions.
The displacement argument can be a float an xyz vector or an nx3 array (where n is the number of atoms).
- wrap(**wrap_kw)[source]#
Wrap positions to unit cell.
Parameters:
- wrap_kw: (keyword=value) pairs
optional keywords \(pbc\), \(center\), \(pretty_translation\), \(eps\), see
ase.geometry.wrap_positions()
