Radiation-Reaction: Self-consistent Light-Matter interaction with real-time TDDFT¶
In this tutorial, we calculate the superradiant absorption-spectrum of a sodium-dimer chain.
The equations underlying the implementation are described in Ref. [1]. The here used parameters are coarser than the published work. This implementation is so far only available for the LCAO mode.
We use real-time TDDFT LCAO mode
and add the radiation-reaction potential for emission into a waveguide.
The available implementation adds a local potential that accounts for the recoil
that emerges as a consequence of the emission of light. This approach effectively
embeds the electromagnetic environment into the KS equation and ensures a
self-consistent interaction between light and matter.
The keyword RRemission demands the cross-sectional area of the waveguide
and the polarization of the propagating electric field.
With decreasing cross-sectional area, the emission will be stronger.
Thus far, 1d-waveguide emission is the only available electromagnetic environment
but further additions are scheduled.
We will start by calculating the emission spectrum in z-direction for a single sodium dimer:
from ase import Atoms
from gpaw import GPAW
from gpaw.lcaotddft import LCAOTDDFT
from gpaw.lcaotddft.qed import RRemission
from gpaw.lcaotddft.dipolemomentwriter import DipoleMomentWriter
from gpaw.tddft.spectrum import photoabsorption_spectrum
# Sodium dimer chain
d = 1.104 # N2 bondlength
L = 8.0 # N2-N2 distance
atoms = Atoms('Na2',
positions=[[L, 0, +d / 2], [L, 0, -d / 2]],
cell=[L, 8.0, 8.0])
atoms.center()
# Ground-state calculation
calc = GPAW(mode='lcao', h=0.3, basis='dzp', xc='LDA',
setups={'Na': '1'},
convergence={'density': 1e-12},
txt='gs_nad.out',
symmetry={'point_group': False})
atoms.calc = calc
energy = atoms.get_potential_energy()
calc.write('gs.gpw', mode='all')
# Time-propagation calculation
# Read converged ground-state file
td_calc = LCAOTDDFT('gs.gpw', rremission=RRemission(35.05, [0, 0, 1]))
# Attach any data recording or analysis tools
DipoleMomentWriter(td_calc, 'dm_nad.dat')
# Kick
td_calc.absorption_kick([0.0, 0.0, 1e-5])
# Propagate
td_calc.propagate(20, 5000)
# Please note that those parameter values are quite course
# and should be properly converged for subsequent applications.
# Calculate spectrum with small artificial broadening
photoabsorption_spectrum('dm_nad.dat', 'spec_nad.dat',
folding='Gauss', width=0.005,
e_min=0.0, e_max=10.0, delta_e=0.005)
The polarization of the electric field in the waveguide is aligned with the z-axis, exerting a recoil-force on the electronic coordinates that oscillate in this direction. As a result, the electronic motion is damped as energy is emitted into the waveguide, in line with Newtons third law.
Let us next add a second dimer parallel to the first one and orthorgonal to the chain-axis (H-aggregate configuration). For reasons that will become clear in the following, we can get away with half the propagation time.
from ase import Atoms
from gpaw import GPAW
from gpaw.lcaotddft import LCAOTDDFT
from gpaw.lcaotddft.qed import RRemission
from gpaw.lcaotddft.dipolemomentwriter import DipoleMomentWriter
from gpaw.tddft.spectrum import photoabsorption_spectrum
# Sodium dimer chain
d = 1.104 # N2 bondlength
L = 8.0 # N2-N2 distance
atoms = Atoms('Na4',
positions=([[L, 0, +d / 2], [L, 0, -d / 2], [2 * L, 0, +d / 2],
[2 * L, 0, -d / 2]]), cell=[L + 2 * L, 8.0, 8.0])
atoms.center()
# Ground-state calculation
calc = GPAW(mode='lcao', h=0.3, basis='dzp', xc='LDA',
setups={'Na': '1'},
convergence={'density': 1e-12},
txt='gs_nad2.out',
symmetry={'point_group': False})
atoms.calc = calc
energy = atoms.get_potential_energy()
calc.write('gs.gpw', mode='all')
# Time-propagation calculation
# Read converged ground-state file
td_calc = LCAOTDDFT('gs.gpw', rremission=RRemission(35.05, [0, 0, 1]))
# Attach any data recording or analysis tools
DipoleMomentWriter(td_calc, 'dm_nad2.dat')
# Kick
td_calc.absorption_kick([0.0, 0.0, 1e-5])
# Propagate
td_calc.propagate(20, 2500)
# Please note that those parameter values are quite course
# and should be properly converged for subsequent applications.
# Calculate spectrum with small artificial broadening
photoabsorption_spectrum('dm_nad2.dat', 'spec_nad2.dat',
folding='Gauss', width=0.005,
e_min=0.0, e_max=10.0, delta_e=0.005)
We smoothed the spectra in both cases with a sharp Lorentzian for visual appearance but the observed width corresponds to the correct lifetimes. In the perturbative limit, this corresponds to Wigner-Weisskop theory. Two features can be observed.
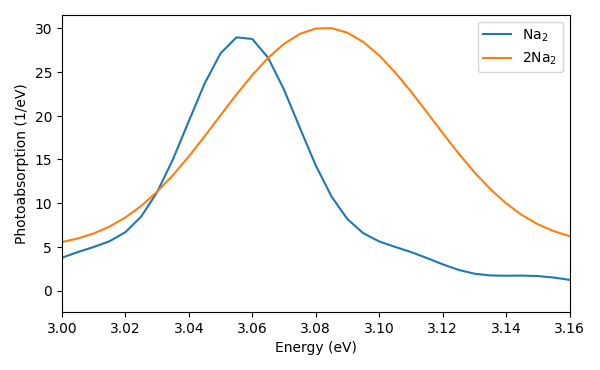
1) The width of two sodium dimers is double the width of a single one. For a set of non-interacting matter-subsystems, their emission probability of a single photon scales linearly with the number of subsystem, i.e., the rate increases here linearly with the number of dimers. Intuitively, more charge oscillating provides a larger dipole which leads to a stronger emission. Clearly, the dimers are not entirely non-interacting for distance of 0.8 nm, which leads to the following observation.
2) The peak is shifted slightly to higher frequencies. The parallel configuration between the dimers results in a coupling between the dipolar excitations that shift the excitation energy to slightly higher values. This configuration is also known as H-aggregate. A head to end configuration on the other hand is known as J-aggregate, providing a red-shift.
It is important to realize here that the propagation time has to be long enough to allow the recoil-forces to substantially damp the oscillations, i.e., enough time is needed to capture the decay.
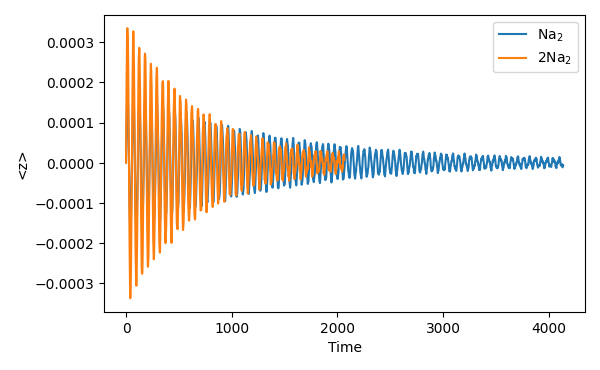
Often this might be unfeasible or unsuitable such that an extrapolation from small cross-sectional areas and quick decay to larger areas and slower decay might be beneficial. A generalized implementation, including strong coupling and complex electromagnetic environments is currently in develop.