X-Ray Absorption Spectroscopy (XAS)¶
Schematic illustration of XAS (from [Nil04]):
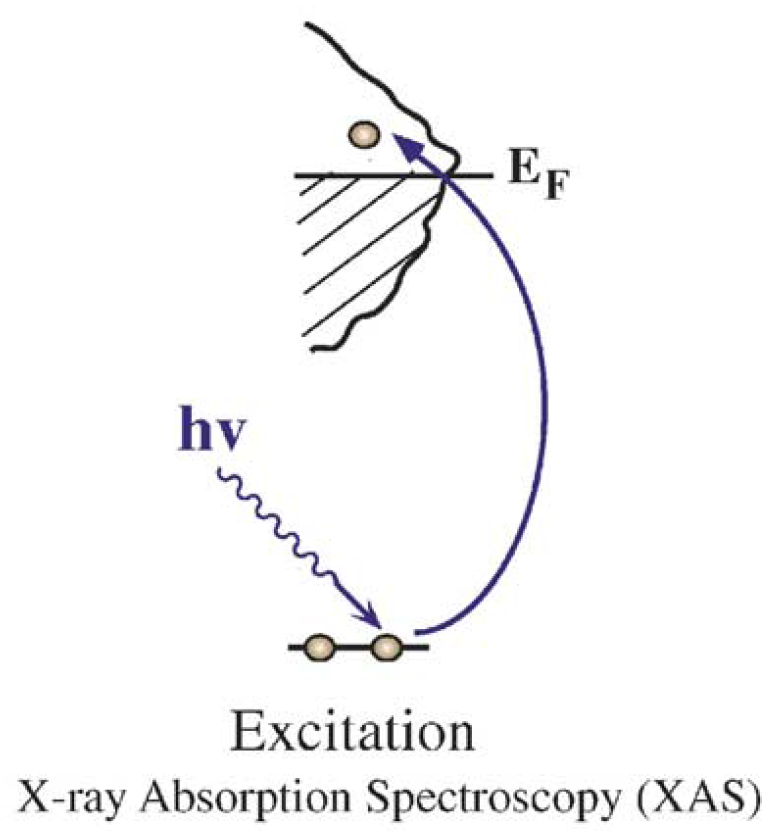
The oscillator strengths are proportional to \(|\langle \phi_{1s}| \mathbf{r} | \psi_n \rangle|^2\), where the one-center expansion of \(\psi_n\) for the core-hole atom can be used.
Introduction¶
The pseudo wave-functions are solutions to this generalized eigenvalue problem:
This can be transformed into a standard eigenvalue problem:
where \(\psi_n = S^{1/2} \tilde{\psi}_n\) is an all-electron wave function.
XAS cross section¶
For the cross section, we need this quantity:
where \(\phi^a\) is the core state localized on atom \(a\) and \(\tilde{\phi}^a = \sum_i \langle \phi_i^a | x | \phi^a \rangle \tilde{p}_i^a\). Now, the cross section is:
By introducing \(G(E) = (E - S^{-1/2} H S^{-1/2} + i \gamma)^{-1}\), we get:
Recursion method¶
Instead of working with the \(u_i\) functions from the Taillefumier paper, we introduce \(w_i=S^{1/2}u_i\) which are the actual functions that we need to find. We now define \(y_i\) and \(z_i\) as:
With these definitions, the recursion formula reads:
where:
and
The \(w_i\) functions should be normalized as:
and the recursion is started with \(w_0 \propto \tilde{\phi}^a\).
Inverting the S matrix¶
The S (or O) operator is defined as:
Where \(O^a_{i_1 i_2} = <\phi ^a_{i_1}| \phi ^a_{i_2}> - <\tilde \phi ^a_{i_1}| \tilde \phi ^a_{i_2}>\)
Assume that \(\hat O^{-1}\) can be written as
Then according to [P.J. Hasnip et al, Comp. Phys. Comm. 174 (2006) 24-29 ] the coefficients \(P^a_{i_1 i_2}\) are given by
With summation over equal indices (except a). These formulas ignore overlap between projectors on different atoms. The accuracy of the \(\hat O^{-1}\) operator can be checked for example by doing:
which should be zero for all normalized, orthogonalized \(\tilde \phi\)