Occupation number smearing

See also

Occupation numbers

Convergence with respect to number of k-point for bulk Cu energy with different smearing methods:

from ase.build import bulk
from gpaw import GPAW, PW

cu = bulk('Cu', 'fcc', a=3.6)

for smearing in [{'name': 'improved-tetrahedron-method'},
                 {'name': 'tetrahedron-method'},
                 {'name': 'fermi-dirac', 'width': 0.05},
                 {'name': 'marzari-vanderbilt', 'width': 0.2}]:
    name = ''.join(word[0].upper() for word in smearing['name'].split('-'))
    width = smearing.get('width')
    if width:
        name += f'-{width}'

    for k in range(8, 21):
        cu.calc = GPAW(
            mode=PW(400),
            kpts=(k, k, k),
            occupations=smearing,
            txt=f'Cu-{name}-{k}.txt')
        e = cu.get_potential_energy()

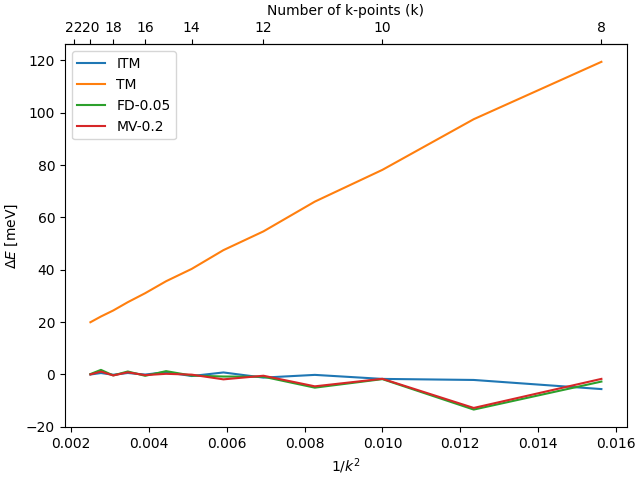
(made with cu_plot.py). See also figure 3 in Blöchl et. al.

gpaw.occupations.create_occ_calc(dct, *, parallel_layout=None, fixed_magmom_value=None, rcell=None, monkhorst_pack_size=None, bz2ibzmap=None, nspins=None, nelectrons=None, nkpts=None, nbands=None)

Surprise: Create occupation-number object.

The unit of width is eV and name must be one of:

• ‘fermi-dirac’

• ‘marzari-vanderbilt’

• ‘methfessel-paxton’

• ‘fixed’

• ‘tetrahedron-method’

• ‘improved-tetrahedron-method’

• ‘orbital-free’

>>> occ = create_occ_calc({'width': 0.0})
>>> occ.calculate(nelectrons=3,
...               eigenvalues=[[0, 1, 2], [0, 2, 3]],
...               weights=[1, 1])
(array([[1., 1., 0.],
       [1., 0., 0.]]), [1.5], 0.0)

gpaw.occupations.fermi_dirac(eig, fermi_level, width)

Fermi-Dirac distribution function.

>>> f, _, _ = fermi_dirac(0.0, 0.0, 0.1)
>>> f
0.5

gpaw.occupations.marzari_vanderbilt(eig, fermi_level, width)

Marzari-Vanderbilt distribution (cold smearing).

See: doi: 10.1103/PhysRevLett.82.3296

gpaw.occupations.methfessel_paxton(eig, fermi_level, width, order=0)

Methfessel-Paxton distribution.

class gpaw.occupations.OccupationNumberCalculator(parallel_layout=None)

Base class for all occupation number calculators.

Object for calculating fermi level(s) and occupation numbers.

If fixmagmom=True then the fixed_magmom_value attribute must be set and two fermi levels will be calculated.

calculate(nelectrons, eigenvalues, weights, fermi_levels_guess=None)

Calculate occupation numbers and fermi level(s) from eigenvalues.

nelectrons:

Number of electrons.

eigenvalues: ndarray, shape=(nibzkpts, nbands)

Eigenvalues in Hartree.

weights: ndarray, shape=(nibzkpts,)

Weights of k-points in IBZ (must sum to 1).

parallel:

Parallel distribution of eigenvalues.

fermi_level_guesses:

Optional guess(es) at fermi level(s).

Returns a tuple containing:

• occupation numbers (in the range 0 to 1)

• fermi-level in Hartree

• entropy as -S*T in Hartree

>>> occ = ZeroWidth()
>>> occ.calculate(1, [[0, 1]], [1])
(array([[1., 0.]]), [0.5], 0.0)

class gpaw.occupations.FixedOccupationNumbers(numbers, parallel_layout=None)

Fixed occupation numbers.

f_sn: ndarray, shape=(nspins, nbands)

Occupation numbers (in the range from 0 to 1)

Example (excited state with 4 electrons):

occ = FixedOccupationNumbers([[1, 0, 1, 0], [1, 1, 0, 0]])

class gpaw.occupations.ParallelLayout(bd, kpt_comm, domain_comm)

Collection of parallel stuff.

Create new instance of ParallelLayout(bd, kpt_comm, domain_comm)

gpaw.occupations.occupation_numbers(occ, eig_skn, weight_k, nelectrons)

Calculate occupation numbers from eigenvalues in eV (deprecated).

occ: dict

Example: {‘name’: ‘fermi-dirac’, ‘width’: 0.05} (width in eV).

eps_skn: ndarray, shape=(nspins, nibzkpts, nbands)

Eigenvalues.

weight_k: ndarray, shape=(nibzkpts,)

Weights of k-points in IBZ (must sum to 1).

nelectrons: int or float

Number of electrons.

Returns a tuple containing:

• f_skn (sums to nelectrons)

• fermi-level [Hartree]

• magnetic moment

• entropy as -S*T [Hartree]

Tetrahedron method

class gpaw.tetrahedron.TetrahedronMethod(rcell, size, improved=False, bz2ibzmap=None, parallel_layout=None)

Tetrahedron method for calculating occupation numbers.

The reciprocal cell, rcell, can be given in arbitrary units (only the shape matters) and size is the size of the Monkhorst-Pack grid. If k-points have been symmetry-reduced the bz2ibzmap parameter mapping BZ k-point indizes to IBZ k-point indices must be given.