Local properties of individual magnetic sites

It is almost always very useful to analyze magnetic systems in terms of the individual magnetic sites of the crystal. In this tutorial, we illustrate how to calculate individual site properties for the magnetic atoms in GPAW.

Since it is not well-defined a priori where one site ends and another begins, GPAW supplies functionality to calculate the site properties as a function of spherical radii \(r_\mathrm{c}\). In this picture, the site properties are defined in terms of integrals with unit step functions \(\Theta(\mathbf{r}\in\Omega_{a})\), which are nonzero only inside a sphere of radius \(r_\mathrm{c}\) around the given magnetic atom \(a\).

Local functionals of the spin-density

For any functional of the (spin-)density \(f[n, \mathbf{m}](\mathbf{r})\), one may define a corresponding site quantity,

\[f_a = \int d\mathbf{r}\: \Theta(\mathbf{r}\in\Omega_{a}) f[n,\mathbf{m}](\mathbf{r}).\]

GPAW supplies functionality to compute such site quantities defined based on local functionals of the spin-density for collinear systems, \(f[n,\mathbf{m}](\mathbf{r}) = f(n(\mathbf{r}),n^z(\mathbf{r}))\). The implementation (using the PAW method) is documented in [1].

In particular, the site magnetization,

\[m_a = \int d\mathbf{r}\: \Theta(\mathbf{r}\in\Omega_{a}) n^z(\mathbf{r}),\]

can be calculated via the function calculate_site_magnetization(), whereas the function calculate_site_zeeman_energy() computes the LSDA site Zeeman energy,

\[E_a^\mathrm{Z} = - \int d\mathbf{r}\: \Theta(\mathbf{r}\in\Omega_{a}) W_\mathrm{xc}^z(\mathbf{r}) n^z(\mathbf{r}).\]

Example: Iron

In the script Fe_site_properties.py, the site magnetization and Zeeman energy are calculated from the ground state of bcc iron. The script should take less than 10 minutes on a 40 core node. After running the calculation script, you can download and excecute Fe_plot_site_properties.py to plot the site magnetization and Zeeman energy as a function of the spherical site radius \(r_\mathrm{c}\).

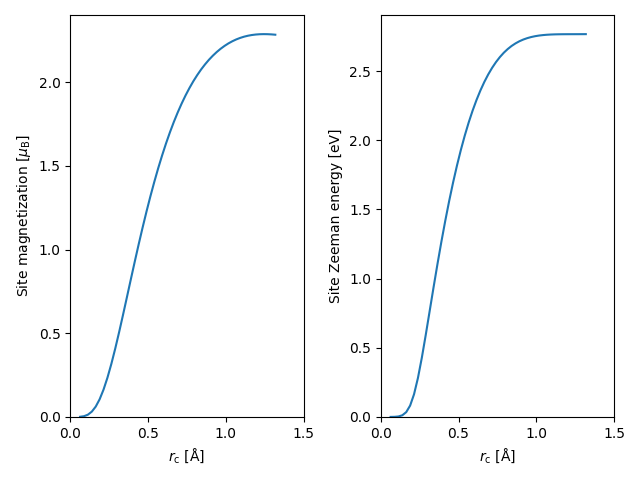
Although there does not exist an a priori magnetic site radius \(r_\mathrm{c}\), we clearly see that there is a region, where the site Zeeman energy is constant as a function of the radius, hence making \(E_a^\mathrm{Z}\) a well-defined property of the system in its own right. However, the same cannot be said for the site magnetization, which continues to varry as a function of the cutoff radius. This is due to the fact that the interstitial region between the Fe atoms is slightly spin-polarized anti-parallely to the local magnetic moments, resulting in a radius \(r_\mathrm{c}^\mathrm{max}\) which maximizes the site magnetization. If one wants to employ a rigid spin approximation for the magnetic site, i.e. to assume that the direction of magnetization is constant within the site volume, it would be a natural choice to use \(r_\mathrm{c}^\mathrm{max}\) to define the sites.

Site-based sum rules

In addition to site quantities, one may also introduce the concept of site matrix elements, that is, expectation values of functionals \(f(\mathbf{r})=f[n, \mathbf{m}](\mathbf{r})\) evaluated on specific spherical sites,

\[f^a_{n\mathbf{k}s,m\mathbf{k}+\mathbf{q}s'} = \langle \psi_{n\mathbf{k}s}| \Theta(\mathbf{r}\in\Omega_{a}) f(\mathbf{r}) |\psi_{m\mathbf{k}+\mathbf{q}s'} \rangle = \int d\mathbf{r}\: \Theta(\mathbf{r}\in\Omega_{a}) f(\mathbf{r})\, \psi_{n\mathbf{k}s}^*(\mathbf{r}) \psi_{m\mathbf{k}+\mathbf{q}s'}(\mathbf{r}).\]

Similar to the site quantities, GPAW includes functionality to calculate site matrix elements for arbitrary local functionals of the (spin-)density \(f(\mathbf{r}) = f(n(\mathbf{r}),n^z(\mathbf{r}))\), with implementational details documented in [1]. For example, one can calculate the site pair density

\[n^a_{n\mathbf{k}s,m\mathbf{k}+\mathbf{q}s'} = \langle \psi_{n\mathbf{k}s}| \Theta(\mathbf{r}\in\Omega_{a}) |\psi_{m\mathbf{k}+\mathbf{q}s'} \rangle\]

as well as the site Zeeman pair energy

\[E^{\mathrm{Z},a}_{n\mathbf{k}s,m\mathbf{k}+\mathbf{q}s'}=- \langle \psi_{n\mathbf{k}s}| \Theta(\mathbf{r}\in\Omega_{a}) W_\mathrm{xc}^z(\mathbf{r}) |\psi_{m\mathbf{k}+\mathbf{q}s'} \rangle.\]

Now, from such site matrix elements, one can formulate a series of sum rules for various site quantities. For instance, one can construct single-particle sum rules for both the site magnetization and the site Zeeman energy, simply by summing over the diagonal of the site matrix elements for all the occupied states, weighted by the Pauli matrix \(\sigma^z\),

\[m_a = \frac{1}{N_k} \sum_\mathbf{k} \sum_{n,s} \sigma^z_{ss} f_{n\mathbf{k}s} n^a_{n\mathbf{k}s,n\mathbf{k}s},\]

\[E_a^\mathrm{Z} = \frac{1}{N_k} \sum_\mathbf{k} \sum_{n,s} \sigma^z_{ss} f_{n\mathbf{k}s} E^{\mathrm{Z},a}_{n\mathbf{k}s,n\mathbf{k}s}.\]

Although trivial, these sum rules can be used as a consistency tests for the implementation and can be accessed via the functions calculate_single_particle_site_magnetization() and calculate_single_particle_site_zeeman_energy().

In addition to the single-particle sum rules, one may also introduce actual pair functions that characterize the band transitions of the system. In particular, one may introduce the so-called pair site magnetization

\[m_{ab}(\mathbf{q}) = \frac{1}{N_k} \sum_\mathbf{k} \sum_{n,m} \left( f_{n\mathbf{k}\uparrow} - f_{m\mathbf{k}+\mathbf{q}\downarrow} \right) n^a_{n\mathbf{k}\uparrow,m\mathbf{k}+\mathbf{q}\downarrow} n^b_{m\mathbf{k}+\mathbf{q}\downarrow,n\mathbf{k}\uparrow}\]

and pair site Zeeman energy

\[E^\mathrm{Z}_{ab}(\mathbf{q}) = \frac{1}{N_k} \sum_\mathbf{k} \sum_{n,m} \left( f_{n\mathbf{k}\uparrow} - f_{m\mathbf{k}+\mathbf{q}\downarrow} \right) E^{\mathrm{Z},a}_{n\mathbf{k}\uparrow,m\mathbf{k}+\mathbf{q}\downarrow} n^b_{m\mathbf{k}+\mathbf{q}\downarrow,n\mathbf{k}\uparrow},\]

which turn out to be \(\mathbf{q}\)-independent diagonal pair functions, \(m_{ab}(\mathbf{q})=\delta_{ab} m_a\) and \(E^{\mathrm{Z}}_{ab}(\mathbf{q})=\delta_{ab} E^\mathrm{Z}_a\), thanks to a simple sum rule [1]. Because the sum rule relies on the completeness of the Kohn-Sham eigenstates, it breaks down when using only a finite number of bands. Hence, it can be useful to study the band convergence of \(m_{ab}(\mathbf{q})\) and \(E^{\mathrm{Z}}_{ab}(\mathbf{q})\) to gain insight about related completeness issues of more complicated pair functions. In GPAW, they can be calculated using the calculate_pair_site_magnetization() and calculate_pair_site_zeeman_energy() functions.

Example: Iron

In the Fe_site_sum_rules.py script, the single-particle site Zeeman energy is calculated along with the pair site Zeeman energy using a varrying number of bands. It should take less than half an hour on a 40 core node to run. Having done so, you can excecute Fe_plot_site_sum_rules.py to plot the band convergence of \(E^{\mathrm{Z}}_{ab}(\mathbf{q})\).

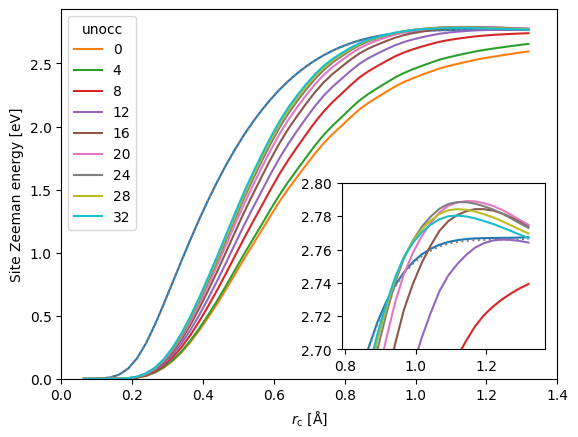
Whereas the single-particle site Zeeman energy (dotted line) is virtually identical to the Zeeman energy calculated from the spin-density (blue line), there are significant deviations from the two-particle site Zeeman energy sum rule, especially with a low number of bands. Including at least 12 bands beyond the 4s and 3d valence bands, we obtain a reasonable fulfillment of the sum rule in the region of radii, where the site Zeeman energy is flat. Interestingly, this is not the case at smaller site radii, meaning that the remaining incompleteness shifts the site Zeeman energy away from the nucleus, while remaining approximately constant when integrating out the entire augmentation sphere.

In the figure, we have left out the imaginary part of the pair site Zeeman energy. You can check yourself that it vanishes more or less identically.

Excercises

To get comfortable with the presented functionality, here are some suggested excercises to get you started:

1. Calculate the site pair magnetization of iron and analyze its band convergence.

2. Investigate the sensitivity of the site pair functions as a function of the wave vector \(\mathbf{q}\).

3. Calculate the site magnetization and spin splitting for a ferromagnetic material with inequivalent magnetic sublattices.

   1. Are you still able to find ranges of radii, where the site Zeeman energy is constant?

   2. What happens to the band convergence of the pair functions?

   3. How does the off-diagonal elements of the pair functions converge as a function of the number of bands?

API

gpaw.response.mft.calculate_site_magnetization(gs, sites)

Calculate the site magnetization.

Returns:

magmom_ap – Magnetic moment in μB of site a under partitioning p, calculated directly from the ground state density.

Return type:

np.ndarray

gpaw.response.mft.calculate_site_zeeman_energy(gs, sites)

Calculate the site Zeeman energy.

Returns:

EZ_ap – Local Zeeman energy in eV of site a under partitioning p, calculated directly from the ground state density.

Return type:

np.ndarray

gpaw.response.mft.calculate_single_particle_site_magnetization(gs, sites, context='-')

Calculate the single-particle site magnetization.

Returns:

sp_magmom_ap – Magnetic moment in μB of site a under partitioning p, calculated based on a single-particle sum rule.

Return type:

np.ndarray

gpaw.response.mft.calculate_single_particle_site_zeeman_energy(gs, sites, context='-')

Calculate the single-particle site Zeeman energy.

Returns:

sp_EZ_ap – Local Zeeman energy in eV of site a under partitioning p, calculated based on a single-particle sum rule.

Return type:

np.ndarray

gpaw.response.mft.calculate_pair_site_magnetization(gs, sites, context='-', q_c=[0.0, 0.0, 0.0], nbands=None)

Calculate the pair site magnetization.

Parameters:

• q_c (Vector) – q-vector to evaluate the pair site magnetization for.

• nbands (int or None) – Number of bands to include in the band summation of the pair site magnetization. If nbands is None, it includes all bands.

Returns:

magmom_abp – Pair magnetization in μB of site a and b under partitioning p, calculated based on a two-particle sum rule.

Return type:

np.ndarray

gpaw.response.mft.calculate_pair_site_zeeman_energy(gs, sites, context='-', q_c=[0.0, 0.0, 0.0], nbands=None)

Calculate the pair site Zeeman energy.

Parameters:

• q_c (Vector) – q-vector to evaluate the pair site Zeeman energy for.

• nbands (int or None) – Number of bands to include in the band summation of the pair site Zeeman energy. If nbands is None, it includes all bands.

Returns:

EZ_abp – Local pair Zeeman energy in eV of site a and b under partitioning p, calculated based on a two-particle sum rule.

Return type:

np.ndarray

References

[1] (1,2,3)

T. Skovhus and T. Olsen, publication in preparation, (2024)