Bare Coulomb potential for hydrogen

Using plane waves

GPAW has a special PAW setup for hydrogen called ae for all-electron. It’s not really a PAW setup because it doesn’t make use of any PAW magic at all — it’s just the bare Coulomb potential (\(-1/r\)).

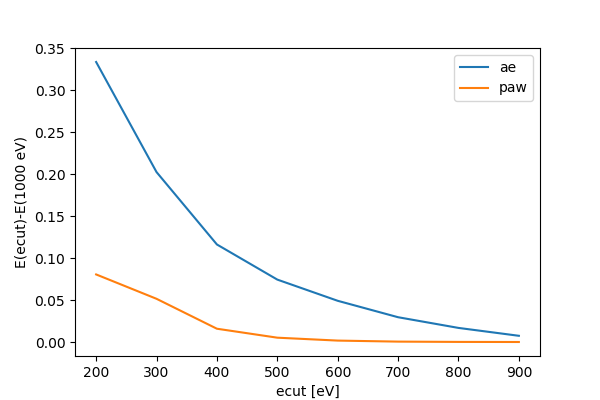
The convergence of the energy as a function of plane-wave cutoff energy will be very slow due to the divergence of the potential at the hydrogen nucleus and also because of the cusp in the wave function:

from ase import Atoms
from gpaw import GPAW, PW
h = Atoms('H', cell=(5, 5, 5))
h.center()
for ecut in range(200, 1001, 100):
    h.calc = GPAW(setups='ae',
                  mode=PW(ecut),
                  txt=f'H-{ecut}-ae.txt')
    e = h.get_potential_energy()

You can look at the energy convergence with this command:

$ ase gui H.ae.txt

Let’s do the same calculation with a PAW setup. Replace the h.calc = line with this:

h.calc = GPAW(mode='fd', txt='H.paw.txt')

Now the energy is converged much quicker:

Using a 1-d radial grid

Since the H atom is spherically symmetric, one can solve the problem on a 1-d grid. You can do that on the command line like this:

$ gpaw atom H -p