Maximizing performance on BG/P¶
Begin by reading up on the GPAW parallelization strategies (Parallel runs) and the BG/P architecture. In particular, Band parallelization will be needed to scale your calculation to large number of cores. The BG/P systems at the Argonne Leadership Computing Facility uses Cobalt for scheduling and it will be referred to frequently below. Other schedulers should have similar functionality.
There are four key aspects that require careful considerations:
Choosing a parallelization strategy.
Selecting the correct partition size (number of nodes) and mapping.
Choosing an appropriate value of
buffer_size. The use ofnblocksis no longer recommended.Setting the appropriate DCMF environmental variables.
In the sections that follow, we aim to cultivate an understanding of how to choose these parameters.
Parallelization Strategy¶
Parallelization options are specified at the gpaw-python command
line. Domain decomposition with --domain-decomposition=Nx,Ny,Nz
and band parallelization with --state-parallelization=B.
Additionally, the parallel keyword is also available.
The smallest calculation that can benefit from band/state parallelization is nbands = 1000. If you are using fewer bands, you are possibly not in need of a leadership class computing facility. Note that only Residual minimization method eigensolver is compatible with band parallelization. Furthermore, the RMM-DIIS eigensolver requires some unoccupied bands in order to converge properly. Recommend range is:
spinpol=False
nbands = valence electrons/2*[1.0 - 1.2]
spinpol=True
nbands = max(up valence electrons, down valence electrons)*[1.0 - 1.2]
It was empirically determined that you need to have nbands/B > 256 for reasonable performance. It is also possible use smaller groups, nbands/B < 256, but this may require large domains. It is required that nbands/B be integer-divisible. The best values for B =2, 4, 8, 16, 32, 64, and 128.
Obviously, the number of total cores must equal:
Nx*Ny*Nz*B
The parallelization strategy will require careful consideration of the partition size and mapping. And, obviously, also memory!
Partition size and Mapping¶
The BG/P partition dimensions (Px, Py, Pz, T) for Surveyor and Intrepid at the Argonne Leadership Computing Facility are available here, where T represents the number of MPI tasks per node (not whether a torus network is available). The number of cores per node which execute MPI tasks is specified by the Cobalt flag:
--mode={smp,dual,vn}
Hence, the possible values of T are:
T = 1 for smp
T = 2 for dual
T = 4 for vn
Note that there are 4 cores per node and 2 GB per node on BG/P. As GPAW is presently an MPI-only code, vn mode is preferred since all cores will perform computational work.
It is essential to think of the BG/P network as a 4-dimensional object with 3 spatial dimensions and a T-dimension. For optimum scalability it would seem necessary to maximize the locality of two distinct communications patterns arising in the canonical O(N^3) DFT algorithm:
H*Psi products
parallel matrix multiplies.
However, it turns out that this is not necessary. The mesh network can handle small messages rather efficiently such that the time to send a small message to a nearest-neighbor node versus a node half-way across the machine is comparable. Hence, it is only necessary to optimize the mapping for the communication arising from the parallel matrix multiply which is a simple 1D systolic communication pattern.
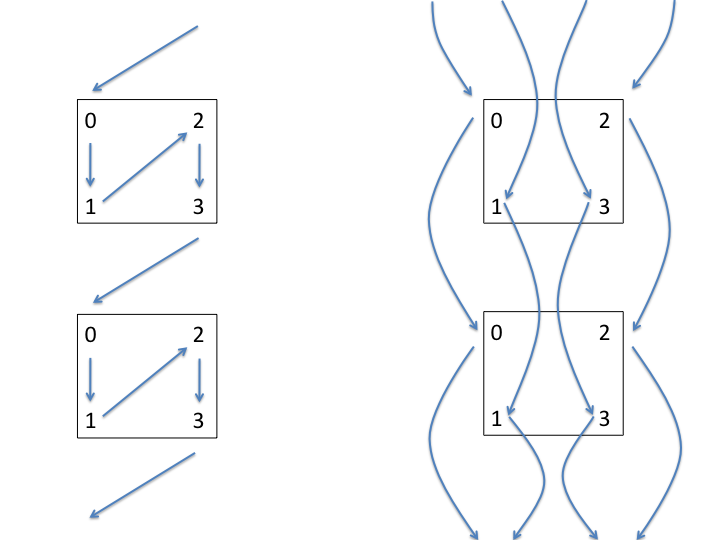
Here we show the examples of different mappings on a 512-node BG/P partition. Band groups are colored coded. (Left) Inefficient mapping for four groups of bands (B = 4). This mapping leads to contention on network links in the z-direction. (Right) Efficient mapping for eight groups of bands (B=8). Correct mapping maximizes scalability and single-core peak performance.
For the mapping on the (Right) above image, there are two communication patterns (and hence mappings) that are worth distinguishing.
The boxes in these images represent a node and the numbers inside the box repesent the distinct cores in the node (four for BG/P). Intuitively, the communication pattern of the (Left) image should lead to less network contention than the (Right). However, this is not the case due to lack of optimization in the intranode implementation of MPI. The performance of these communications patterns is presently identical, though this may change in future version of the BG/P implementation of MPI.
Mapping is accomplished by the Cobalt flag:
--env=BG_MAPPING=<mapping>
where <mapping> can be one of the canonical BG/P mappings (permutations of XYZT with T at the beginning or end) or a mapfile.
Lastly, it is important to note that GPAW orders the MPI tasks as follows:
Z, Y, X, bands, kpoints, and spins.
A list of mappings is provided below. Note that this list is not exhaustive. The contraint on the mapping comes from the value of B; only one of these constraints must be true:
The last dimension in the canonical BG/P mapping equals the value of B.
#) For canonical BG/P mappings which end in T, the product of T and the last cartesian dimension in the mapping equals B.
#) If a canonical mapping is not immediately suitable, the keyword
order in the parallel dictionary can be used to rectify the
problem. See the documentation on Parallel runs.
B = 2¶
Simply set the following variables in your submission script:
mode = dual
mapping = any canonical mapping ending with a T
the constraint on the domain-decomposition is simply:
Nx*Ny*Nz = Px*Py*Pz
B = 4¶
Similar to the B=2 case, but with:
mode = vn
B = 8, 16, 32, 64, or 128¶
This is left as an exercises to the user.
Setting the value of buffer_size¶
Use buffer_size=2048. Refer to Parallelization options for more
information about the buffer_size keyword. Larger values require
increasing the default value of DCMF_RECFIFO.
For those interested in more technical details, continue reading this section.
The computation of the hamiltonian and overlap matrix elements, as well as
the computation of the new wavefunctions, is accomplished by a hand-coded
parallel matrix-multiply hs_operators.py employing a 1D systolic
ring algorithm.
Under the original implementation of the matrix-multiply algorithm,
it was necessary to select appropriate values for the number of blocks nblocks:
from gpaw.hs_operators import MatrixOperator
MatrixOperator.nblocks = K
MatrixOperator.async = True (default)
where the B groups of bands are further divided into K
blocks. It was also required that nbands/B/K be integer-divisible.
The value of K should be chosen so that 2 MB of wavefunctions are
interchanged. The special cases of B=2, 4 as described
above permit the use blocks of wavefunctions larger than 2 MB to be
interchanged since there is only intranode communication.
The size of the wavefunction being interchanged is given by:
gpts = (Gx, Gy, Gz)
size of wavefunction block in MB = (Gx/Nx, Gy/Ny, Gz/Nz)*(nbands/B/K)*8/1024^2
The constraints on the value of nbands are:
nbands/Bmust be integer divisiblenbands/B/Kmust be integer divisible.size of wavefunction block ~ 2 MB
nbandsmust be sufficient largely so that the RMM-DIIS eigensolver converges
The second constraint above is no longer applicable as of SVN version 7520.
Important DCMF environment variables¶
DCMF is one of the lower layers in the BG/P implementation of MPI software stack.
To understand th DCMF environment variables in greater detail, please read the appropriate sections of the IBM System Blue Gene Solution: Blue Gene/P Application Development
DCMF_EAGER and DCMF_RECFIFO¶
Communication and computation is overlapped to the extent allowed by the hardware by using non-blocking sends (Isend) and receives (Irecv). It will be also be necessary to pass to Cobalt:
--env=DCMF_EAGER=8388608
which corresponds to the larger size message that can be overlapped (8 MB). Note that the number is specified in bytes and not megabytes. This is larger than the target 2 MB size, but we keep this for historical reasons since it is possible to use larger blocks of wavefunctions in the case of smp or dual mode. This is also equal to the default size of the DCMF_RECFIFO. If the following warning is obtained,:
A DMA unit reception FIFO is full. Automatic recovery occurs
for this event, but performance might be improved by increasing the FIFO size
the default value of the DCMF_RECFIFO should be increased:
--env=DCMF_RECFIFO=<size in bytes>
DCMF_REUSE_STORAGE¶
If you receive allocation error on MPI_Allreduce, please add the following environment variables:
--env=DCMF_REDUCE_REUSE_STORAGE=N:DCMF_ALLREDUCE_REUSE_STORAGE=N:DCMF_REDUCE=RECT
It is very likely that your calculation is low on memory. Simply try using more nodes.
DCMF_ALLTOALL_PREMALLOC¶
HDF5 uses MPI_Alltoall which can consume a significant amount of memory. The default behavior for MPI collectives on Blue Gene/P is to not release memory between calls due to peformance reasons. We recommend setting this environment variable to overide the default behavior:
--env DCMF_ALLTOALL_PREMALLOC=N: