PBE0 calculations for bulk silicon¶

This tutorial will do non self-consistent PBE0 based on self-consistent PBE.

PBE and PBE0 band gaps¶

The band structure can be calculated like this:

# web-page: si-gaps.csv
from ase.build import bulk
from ase.parallel import paropen
from gpaw.hybrids.eigenvalues import non_self_consistent_eigenvalues
from gpaw import GPAW, PW

a = 5.43
si = bulk('Si', 'diamond', a)

fd = paropen('si-gaps.csv', 'w')

for k in range(2, 9, 2):
    name = f'Si-{k}'
    si.calc = GPAW(kpts={'size': (k, k, k), 'gamma': True},
                   mode=PW(200),
                   xc='PBE',
                   convergence={'bands': 5},
                   txt=name + '.txt')
    si.get_potential_energy()
    si.calc.write(name + '.gpw', mode='all')

    # Range of eigenvalues:
    n1 = 3
    n2 = 5

    ibzkpts = si.calc.get_ibz_k_points()
    kpt_indices = []
    for kpt in [(0, 0, 0), (0.5, 0.5, 0)]:  # Gamma and X
        # Find k-point index:
        i = abs(ibzkpts - kpt).sum(1).argmin()
        kpt_indices.append(i)

    # Do PBE0 calculation:
    epbe, vpbe, vpbe0 = non_self_consistent_eigenvalues(
        name + '.gpw',
        'PBE0',
        n1, n2,
        kpt_indices,
        snapshot=name + '.json')

    epbe0 = epbe - vpbe + vpbe0

    gg = epbe[0, 0, 1] - epbe[0, 0, 0]
    gx = epbe[0, 1, 1] - epbe[0, 0, 0]
    gg0 = epbe0[0, 0, 1] - epbe0[0, 0, 0]
    gx0 = epbe0[0, 1, 1] - epbe0[0, 0, 0]

    print(f'{k}, {gg:.3f}, {gx:.3f}, {gg0:.3f}, {gx0:.3f}', file=fd)
    fd.flush()

assert abs(gg - 2.559) < 0.01
assert abs(gx - 0.707) < 0.01
assert abs(gg0 - 3.873) < 0.01
assert abs(gx0 - 1.828) < 0.01

These are the resulting \(\Gamma\)-\(\Gamma\) and \(\Gamma\)-\(X\) gaps for PBE and PBE0 in eV:

k-points	PBE(G-G)	PBE(G-X)	PBE0(G-G)	PBE0(G-X)
2	2.445	0.598	4.187	2.153
4	2.538	0.688	3.954	1.913
6	2.553	0.701	3.892	1.849
8	2.555	0.704	3.874	1.831

Lattice constant and bulk modulus¶

Here is how to calculate the lattice constant:

import ase.db
from ase.build import bulk
import numpy as np
from gpaw.hybrids.energy import non_self_consistent_energy as nsc_energy
from gpaw import GPAW, PW

a0 = 5.43

con = ase.db.connect('si.db')

for k in range(2, 9):
    for a in np.linspace(a0 - 0.04, a0 + 0.04, 5):
        id = con.reserve(a=a, k=k)
        if id is None:
            continue
        si = bulk('Si', 'diamond', a)
        si.calc = GPAW(kpts=(k, k, k),
                       mode=PW(400),
                       xc='PBE',
                       eigensolver='rmm-diis',
                       txt=None)
        si.get_potential_energy()
        name = f'si-{a:.2f}-{k}'
        si.calc.write(name + '.gpw', mode='all')
        epbe0 = nsc_energy(name + '.gpw', 'PBE0').sum()

        con.write(si, a=a, k=k, epbe0=epbe0)
        del con[id]

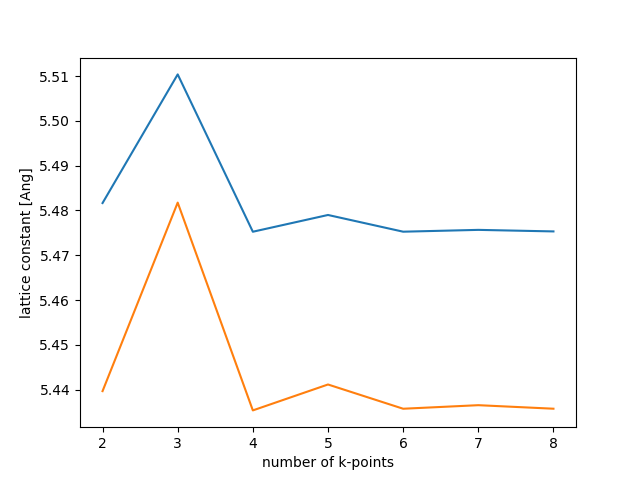
Plot the results like this:

# web-page: si-a.png
import matplotlib.pyplot as plt
import ase.db
from ase.eos import EquationOfState


def lattice_constant(volumes, energies):
    eos = EquationOfState(volumes, energies)
    v, e, B = eos.fit()
    a = (v * 4)**(1 / 3)
    return a


con = ase.db.connect('si.db')
results = []
K = list(range(2, 9))
A = []
A0 = []
for k in K:
    rows = list(con.select(k=k))
    V = [row.volume for row in rows]
    E = [row.energy for row in rows]
    E0 = [row.epbe0 for row in rows]
    A.append(lattice_constant(V, E))
    A0.append(lattice_constant(V, E0))

print(K, A, A0)

plt.plot(K, A, label='PBE')
plt.plot(K, A0, label='PBE0')
plt.xlabel('number of k-points')
plt.ylabel('lattice constant [Ang]')
plt.savefig('si-a.png')